题目内容
已知圆M: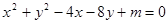 与
与 轴相切。
轴相切。
(1)求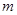 的值;
的值;
(2)求圆M在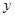 轴上截得的弦长;
轴上截得的弦长;
(3)若点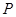 是直线
是直线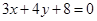 上的动点,过点
上的动点,过点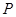 作直线
作直线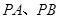 与圆M相切,
与圆M相切,
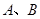 为切点。求四边形
为切点。求四边形 面积的最小值。
面积的最小值。
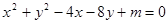 与
与 轴相切。
轴相切。(1)求
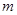 的值;
的值;(2)求圆M在
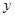 轴上截得的弦长;
轴上截得的弦长;(3)若点
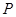 是直线
是直线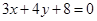 上的动点,过点
上的动点,过点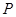 作直线
作直线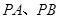 与圆M相切,
与圆M相切,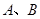 为切点。求四边形
为切点。求四边形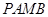 面积的最小值。
面积的最小值。(1)4(2)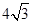 (3)
(3)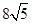
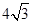 (3)
(3)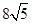
试题分析:(1)令
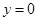 ,有
,有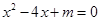 ,由题意知,
,由题意知,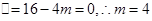
即
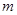 的值为4. 4分
的值为4. 4分(2)设
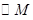 与
与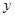 轴交于
轴交于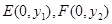 ,令
,令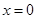 有
有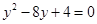 (
( ),
),则
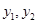 是(
是(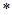 )式的两个根,则
)式的两个根,则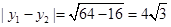 。
。所以
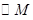 在
在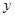 轴上截得的弦长为
轴上截得的弦长为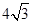 。 9分
。 9分 (3)由数形结合知:
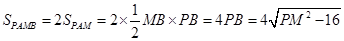 , 10分
, 10分 PM的最小值等于点M到直线
PM的最小值等于点M到直线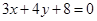 的距离 11分
的距离 11分即
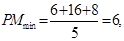 12分
12分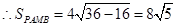 ,即四边形PAMB的面积的最小值为
,即四边形PAMB的面积的最小值为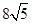 。 14分
。 14分点评:直线与圆相切时,圆心到直线的距离等于圆的半径,直线与圆相交时,圆心到直线的距离,圆的半径,弦长的一半构成直角三角形,此三角形在直线与圆相交的题目中经常用到,第三问结合图形将面积的最小值转化为圆心到直线上的动点的距离最小

练习册系列答案
相关题目
 的圆,经过点
的圆,经过点 ,则该圆的标准方程是
,则该圆的标准方程是




 两点,圆心在x轴上,则圆C的方程是
两点,圆心在x轴上,则圆C的方程是





 ,在上任取一点
,在上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 .设是长为2的线段,点集
.设是长为2的线段,点集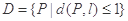 所表示图形的面积为( )
所表示图形的面积为( )

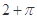

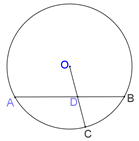
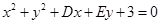 关于直线
关于直线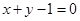 对称,圆心在第二象限,半径为
对称,圆心在第二象限,半径为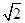
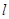 ,
, 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: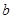 的取值范围;
的取值范围;