题目内容
如图,圆 O 的割线 PBA 过 圆心 O,弦 CD 交 PA 于点F,且△COF∽△PDF,PB =" OA" = 2,则PF = 

3
试题分析:解:∵PB=OA=2,∴OC=OB=2,由相交弦定理得:DF•CF=AF•BF,又∵△COF∽△PDF,∴DF•CF=OF•PF,即AF•BF=OF•PF,即(4-BF)•BF=(2-BF)•(2+BF),解得BF=1,故PF=PB+BF=3,故答案为:3
点评:本题考查的知识点是相交弦定理及相似三角形的性质,其中根据相交弦定理及三角形相似的性质,得到AF•BF=OF•PF,是解答本题的关键

练习册系列答案
相关题目
 的一个焦点为圆心,离心率为半径的圆的方程是( )
的一个焦点为圆心,离心率为半径的圆的方程是( )


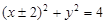
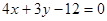 截圆心在点
截圆心在点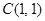 的圆
的圆 所得弦长为
所得弦长为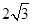 .
. 的圆
的圆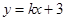 与圆
与圆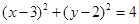 相交于
相交于 ,
, 两点,且
两点,且 ,则
,则 的取值范围是( )
的取值范围是( )
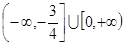

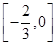
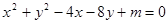 与
与 轴相切。
轴相切。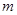 的值;
的值;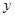 轴上截得的弦长;
轴上截得的弦长;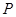 是直线
是直线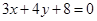 上的动点,过点
上的动点,过点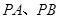 与圆M相切,
与圆M相切,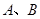 为切点。求四边形
为切点。求四边形 面积的最小值。
面积的最小值。 ,
, ,
, ,
,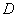 四点共圆,
四点共圆,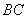 与
与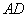 的延长线交于点
的延长线交于点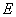 ,点
,点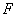 在
在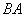 的延长线上.
的延长线上.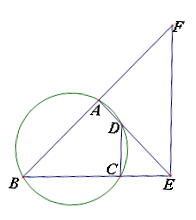
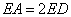 ,
,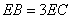 ,求
,求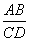 的值;
的值;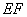 ∥
∥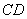 ,求证:线段
,求证:线段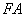 ,
,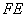 ,
,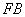 成等比数列.
成等比数列. 上的点到直线
上的点到直线 距离的最大值是( )
距离的最大值是( )