题目内容
(本小题满分14分)
已知椭圆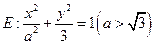 的离心率
的离心率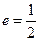 . 直线
. 直线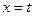 (
(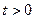 )与曲线
)与曲线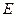 交于不同的两点
交于不同的两点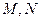 ,以线段
,以线段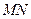 为直径作圆
为直径作圆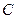 ,圆心为
,圆心为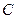 .
.
(1) 求椭圆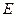 的方程;
的方程;
(2) 若圆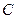 与
与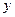 轴相交于不同的两点
轴相交于不同的两点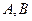 ,求
,求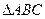 的面积的最大值.
的面积的最大值.
已知椭圆
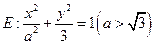 的离心率
的离心率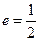 . 直线
. 直线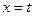 (
(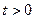 )与曲线
)与曲线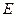 交于不同的两点
交于不同的两点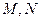 ,以线段
,以线段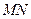 为直径作圆
为直径作圆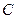 ,圆心为
,圆心为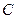 .
. (1) 求椭圆
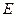 的方程;
的方程;(2) 若圆
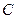 与
与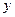 轴相交于不同的两点
轴相交于不同的两点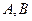 ,求
,求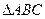 的面积的最大值.
的面积的最大值.(1)解:∵椭圆
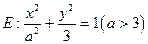 的离心率
的离心率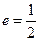 ,
,∴
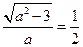 . …… 2分
. …… 2分解得
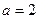 .
.∴ 椭圆
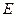 的方程为
的方程为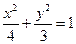 . …… 4分
. …… 4分(2)解法1:依题意,圆心为
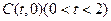 .
.由
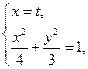 得
得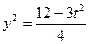 .
. ∴ 圆
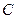 的半径为
的半径为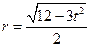 . …… 6分
. …… 6分∵ 圆
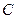 与
与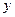 轴相交于不同的两点
轴相交于不同的两点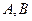 ,且圆心
,且圆心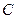 到
到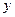 轴的距离
轴的距离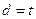 ,
,∴
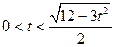 ,即
,即 .
. ∴ 弦长
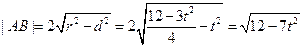 . …… 8分
. …… 8分∴
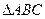 的面积
的面积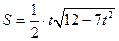 …… 9分
…… 9分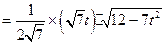
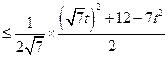
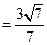 . …… 12分
. …… 12分当且仅当
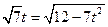 ,即
,即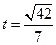 时,等号成立.
时,等号成立.∴
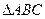 的面积的最大值为
的面积的最大值为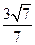 . …… 14分
. …… 14分解法2:依题意,圆心为
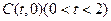 .
.由
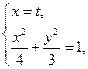 得
得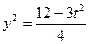 .
.∴ 圆
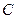 的半径为
的半径为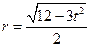 . …… 6分
. …… 6分∴ 圆
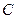 的方程为
的方程为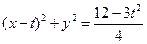 .
.∵ 圆
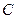 与
与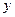 轴相交于不同的两点
轴相交于不同的两点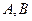 ,且圆心
,且圆心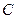 到
到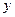 轴的距离
轴的距离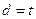 ,
,∴
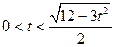 ,即
,即 .
.在圆
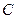 的方程
的方程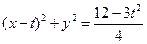 中,令
中,令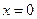 ,得
,得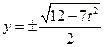 ,
,∴ 弦长
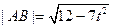 . …… 8分
. …… 8分∴
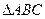 的面积
的面积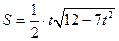 …… 9分
…… 9分 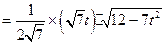
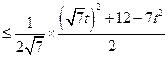
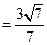 . ……12分
. ……12分当且仅当
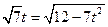 ,即
,即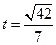 时,等号成立.
时,等号成立.∴
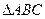 的面积的最大值为
的面积的最大值为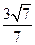 . …… 14分
. …… 14分略

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
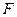 是椭圆
是椭圆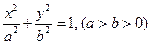 的左焦点,直线
的左焦点,直线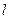 为对应的准线,直线
为对应的准线,直线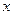 轴交于
轴交于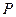 点,
点,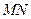 为椭圆的长轴,已知
为椭圆的长轴,已知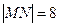 ,且
,且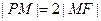 .
.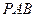 ,恒有
,恒有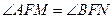 ;
;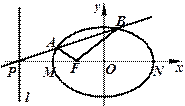
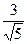 ,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.
,焦点坐标分别为F1(-2,0),F2(2,0),O是坐标原点.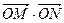 的值;
的值;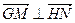 ,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.
,(s<k),分别以线段OG、OH为边作两个正方形,求这两上正方形的面积和的最小值,并求出取得最小值时G、H两点的坐标.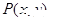 是曲线
是曲线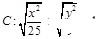 上的点,
上的点,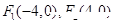 ,则
,则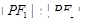 ( )
( )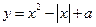 有两个交点,则
有两个交点,则 的取值范围是
的取值范围是 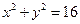 上任一点连线的中点轨迹方程是
上任一点连线的中点轨迹方程是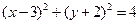
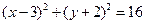
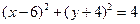
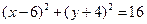
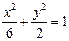 和双曲线
和双曲线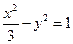 的公共点为
的公共点为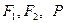 是两曲线的一个交点, 那么
是两曲线的一个交点, 那么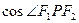 的值是___________
的值是___________