Question

8．已知向量$\overrightarrow{m}$=（sin（x-$\frac{π}{6}$），cosx），$\overrightarrow{n}$=（cosx，cosx），若函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{4}$．
（1）求x∈[-$\frac{π}{4}$，$\frac{π}{2}$]时，函数f（x）的值域；
（2）在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，若f（A）=$\frac{1}{4}$，且|$\overrightarrow{AC}$-$\overrightarrow{AB}$|=2，求BC边上中线长的最大值．

Answer 1

分析 （1）由平面向量数量积的运算及三角函数中的恒等变换应用化简可得f（x）=$\frac{1}{2}$sin（2x+$\frac{π}{6}$），由x∈[-$\frac{π}{4}$，$\frac{π}{2}$]，利用正弦函数的性质即可求得函数f（x）的值域；
（2）由f（A）=$\frac{1}{2}$sin（2A+$\frac{π}{6}$）=$\frac{1}{4}$，解得：sin（2A+$\frac{π}{6}$）=$\frac{1}{2}$，结合范围0＜A＜π，解得：A=$\frac{π}{3}$，由题意可得${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}-2\overrightarrow{AC}•\overrightarrow{AB}=4$，求得|$\overrightarrow{AB}$||$\overrightarrow{AC}$|≤4，从而可求|$\overrightarrow{AD}$|²=$\frac{1}{4}$（$\overrightarrow{AB}+\overrightarrow{AC}$）²=$\frac{1}{4}$（${\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}+|\overrightarrow{AB}||\overrightarrow{AC}|$）=$\frac{1}{4}$（4+2|$\overrightarrow{AB}$||$\overrightarrow{BC}$|）≤3，即可得解．

解答 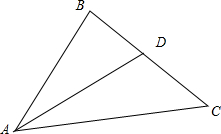解：（1）∵$\overrightarrow{m}$=（sin（x-$\frac{π}{6}$），cosx），$\overrightarrow{n}$=（cosx，cosx），
∴f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{4}$=sin（x-$\frac{π}{6}$）cosx+cos²x-$\frac{1}{4}$=$\frac{\sqrt{3}}{4}$sin2x+$\frac{1+cos2x}{4}$-$\frac{1}{4}$=$\frac{1}{2}$sin（2x+$\frac{π}{6}$），
∵x∈[-$\frac{π}{4}$，$\frac{π}{2}$]，2x+$\frac{π}{6}$∈[-$\frac{π}{3}$，$\frac{7π}{6}$]，
∴f（x）=$\frac{1}{2}$sin（2x+$\frac{π}{6}$）∈[-$\frac{\sqrt{3}}{4}$，$\frac{1}{2}$]．
（2）∵f（A）=$\frac{1}{2}$sin（2A+$\frac{π}{6}$）=$\frac{1}{4}$，解得：sin（2A+$\frac{π}{6}$）=$\frac{1}{2}$，
∵0＜A＜π，$\frac{π}{6}$＜2A+$\frac{π}{6}$＜$\frac{13π}{6}$，
∴2A+$\frac{π}{6}$=$\frac{5π}{6}$，解得：A=$\frac{π}{3}$，
∵|$\overrightarrow{AC}$-$\overrightarrow{AB}$|=2，
∴|$\overrightarrow{AC}$-$\overrightarrow{AB}$|²=4，即${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}-2\overrightarrow{AC}•\overrightarrow{AB}=4$，
∴${\overrightarrow{AC}}^{2}+{\overrightarrow{AB}}^{2}-|\overrightarrow{AC}||\overrightarrow{AB}|=4$，
∴|$\overrightarrow{AB}$||$\overrightarrow{AC}$|≤4，
∴|$\overrightarrow{AD}$|²=$\frac{1}{4}$（$\overrightarrow{AB}+\overrightarrow{AC}$）²=$\frac{1}{4}$（${\overrightarrow{AB}}^{2}+{\overrightarrow{AC}}^{2}+|\overrightarrow{AB}||\overrightarrow{AC}|$）=$\frac{1}{4}$（4+2|$\overrightarrow{AB}$||$\overrightarrow{BC}$|）≤3，
∴|$\overrightarrow{AD}$|_max=$\sqrt{3}$．

点评 本题主要考查了三角函数中的恒等变换应用，平面向量数量积的运算，利用平面向量数量积的运算求中线AD是解题的关键，属于基本知识的考查．