题目内容
17.已知函数f(x)=lnx+$\frac{a}{x}$-1,x轴是函数图象的一条切线.(1)求a;
(2)已知x∈(0,+∞),求证:ln($\frac{x+1}{x}$)>$\frac{1}{x+1}$;
(3)已知:n∈N,n≥2,求证:lnn>$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{n}$.
分析 (1)由x轴是函数f(x)图象的一条切线,得0是函数f(x)的一个极小值,由导数可得x=a是函数的极小值点,则由f(a)=0求得a值;
(2)由(1)得:f(x)=lnx+$\frac{1}{x}-1$=$\frac{1-x}{x}$+lnx在(1,+∞)上为增函数,结合f(1)=0,得到lnx>1-$\frac{1}{x}$在(1,+∞)上恒成立,以$\frac{x+1}{x}$替换x得答案;
(3)由lnx>1-$\frac{1}{x}$在(1,+∞)上恒成立,得ln2>$\frac{1}{2}$,ln$\frac{3}{2}$>$\frac{1}{3}$,ln$\frac{4}{3}$>$\frac{1}{4}$,…,ln$\frac{n}{n-1}$>$\frac{1}{n}$,累加得:ln2+ln$\frac{3}{2}$+…+ln$\frac{n}{n-1}$=lnn>$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{n}$.
解答 (1)解:由f(x)=lnx+$\frac{a}{x}$-1,得f′(x)=$\frac{1}{x}-\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
∵x轴是函数f(x)图象的一条切线,
∴0是函数f(x)的一个极小值.
当a≤0时,f′(x)≥0,函数在定义域(0,+∞)上为增函数,无极值;
∴a>0.
当x∈(0,a)时,f′(x)<0,f(x)为减函数;
当x∈(a,+∞)时,f′(x)>0,f(x)为增函数.
∴x=a为函数的极小值点,则f(a)=$lna+\frac{a}{a}-1=0$,即a=1;
(2)证明:由(1)得:f(x)=lnx+$\frac{1}{x}-1$=$\frac{1-x}{x}$+lnx在(1,+∞)上为增函数,
又由f(1)=0,
故f(x)=$\frac{1-x}{x}$+lnx>0在(1,+∞)上恒成立,
即lnx>$\frac{x-1}{x}$在(1,+∞)上恒成立,
∴lnx>1-$\frac{1}{x}$在(1,+∞)上恒成立,
由x>0,得$\frac{x+1}{x}>1$,
∴$ln(\frac{x+1}{x})>1-\frac{1}{\frac{x+1}{x}}=1-\frac{x}{x+1}=\frac{1}{x+1}$;
(3)证明:∵lnx>1-$\frac{1}{x}$在(1,+∞)上恒成立,
∴ln2>$\frac{1}{2}$,
ln$\frac{3}{2}$>$\frac{1}{3}$,
ln$\frac{4}{3}$>$\frac{1}{4}$,
…,
ln$\frac{n}{n-1}$>$\frac{1}{n}$,
累加得:ln2+ln$\frac{3}{2}$+…+ln$\frac{n}{n-1}$=lnn>$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{n}$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的最值,训练了利用导数证明不等式的方法,体现了数学转化思想方法,是压轴题.

 习题精选系列答案
习题精选系列答案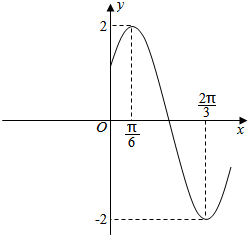 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.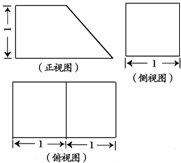 一几何体的三视图如图所示.
一几何体的三视图如图所示.