题目内容
20．已知f（x）=$\left\{\begin{array}{l}{（3-a）x+2，x≤2}\\{{a}^{{2x}^{2}-9x+11}，x＞2}\end{array}\right.$（a＞0，a≠1），数列{an}满足an=f（n），且{an}是递增数列，则a的取值范围为[2，3）．分析 由{an}是递增数列，可得$\left\{\begin{array}{l}{3-a＞0}\\{a＞1}\\{f（2）＜f（3）}\end{array}\right.$，解出即可．
解答 解：∵{an}是递增数列，
∴$\left\{\begin{array}{l}{3-a＞0}\\{a＞1}\\{（3-a）×2+2≤{a}^{2×{3}^{2}-9×3+11}}\end{array}\right.$，
解得2≤a＜3，
∴a的取值范围为[2，3）．
故答案为：[2，3）．
点评 本题考查了数列的单调性、一次函数的单调性、指数函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
15．非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$|$\overrightarrow{b}$|，且（$\overrightarrow{a}-\overrightarrow{b}$）⊥（2$\overrightarrow{a}$+3$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{2π}{3}$ | D． | $\frac{3π}{4}$ |
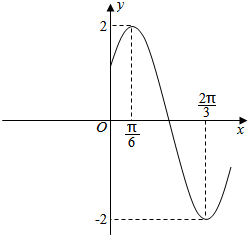函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示．