题目内容

20．求证：函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x（x≥0）}\\{-{x}^{2}+2x（x＜0）}\end{array}\right.$是R上的奇函数．

分析 由奇函数的定义，证明f（-x）=-f（x）即可．

解答 证明：设x＞0，则-x＜0，∴f（-x）=x2-2x=-f（x），
同理x＜0时，f（-x）=-f（x），
又f（0）=0，
∴函数是奇函数．

点评 本题考查函数奇偶性的证明，属基础知识的考查，较简单．

练习册系列答案
相关题目
10．设x，y满足约束条件$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$，分别求出：
（1）z=$\frac{y}{x}$的最大值，最小值；
（2）z=|x-4y+1|的最大值，最小值．
11．已知X={x|-1＜x＜5}，Y={x|x-a＞0}，若X∩Y=∅，求a．
8．设函数f（x）是定义在（-∞，+∞）上的减函数，当不等式组$\left\{\begin{array}{l}{f（1+kx-{x}^{2}）＞f（k+2）}\\{f（3kx-1）＞f（1+kx-{x}^{2}）}\end{array}\right.$对任意的x∈[0，1]都成立时，求k的取值范围．
15．非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$|$\overrightarrow{b}$|，且（$\overrightarrow{a}-\overrightarrow{b}$）⊥（2$\overrightarrow{a}$+3$\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为（　　）
A．$\frac{π}{3}$B．$\frac{π}{4}$C．$\frac{2π}{3}$D．$\frac{3π}{4}$
1．斐波那契数列{an}为1，1，2，3，5，8…，已知S${\;}_{{a}_{n}}$为数列{an}的前n项和，则$\frac{{S}_{{a}_{2015}}}{{a}_{2015}}$=$\frac{（\frac{1+\sqrt{5}}{2}）^{2017}-（\frac{1-\sqrt{5}}{2}）^{2017}-\sqrt{5}}{（\frac{1+\sqrt{5}}{2}）^{2015}-（\frac{1-\sqrt{5}}{2}）^{2015}}$．
8．已知向量$\overrightarrow{m}$=（sin（x-$\frac{π}{6}$），cosx），$\overrightarrow{n}$=（cosx，cosx），若函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{4}$．
（1）求x∈[-$\frac{π}{4}$，$\frac{π}{2}$]时，函数f（x）的值域；
（2）在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，若f（A）=$\frac{1}{4}$，且|$\overrightarrow{AC}$-$\overrightarrow{AB}$|=2，求BC边上中线长的最大值．
5．已知正数列{an}，Sn=$\frac{1}{8}$（an+2）2．
（1）求证：{an}是等差数列；
（2）求数列{an}的通项公式．
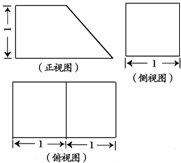6．一几何体的三视图如图所示．
（1）试画出它的直观图；
（2）求它的表面积和体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网