题目内容

18．不等式$\frac{4-x}{-{x}^{2}-4x-4}$＜0的解集是（　　）
A．（-∞，4）B．（4，+∞）C．（-∞，4）∪（4，+∞）D．（-∞，-2）∪（-2，4）

分析 原不等式可化为x-4＜0且x≠-2，综合可得解集．

解答 解：原不等式可化为$\frac{x-4}{（x+2）^{2}}$＜0，
可得x≠-2，（x+2）2＞0，
∴不等式可化为x-4＜0，解得x＜4，
∴不等式的解集为{x|x＜4且x≠-2}，
即（-∞，-2）∪（-2，4），
故选：D．

点评 本题考查分式不等式的解集，属基础题．

练习册系列答案
相关题目
8．已知向量$\overrightarrow{m}$=（sin（x-$\frac{π}{6}$），cosx），$\overrightarrow{n}$=（cosx，cosx），若函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{4}$．
（1）求x∈[-$\frac{π}{4}$，$\frac{π}{2}$]时，函数f（x）的值域；
（2）在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，若f（A）=$\frac{1}{4}$，且|$\overrightarrow{AC}$-$\overrightarrow{AB}$|=2，求BC边上中线长的最大值．
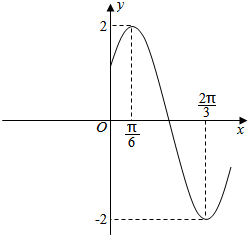9．函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示．
（1）求y的表达式．
（2）求函数的单调增区间与对称中心．
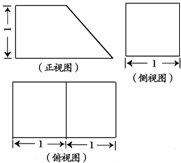6．一几何体的三视图如图所示．
（1）试画出它的直观图；
（2）求它的表面积和体积．
13．过点（-2，1）且与圆x2+2x+y2=0相切的直线方程为x=-2或y=1．
3．已知函数y=-x2+ax-$\frac{a}{4}$+$\frac{1}{2}$．
（1）当0≤x≤1时，函数随着x的增大而增大，求实数a的取值范围；
（2）当0≤x≤1时，函数的最大值是2，求实数a的值．
10．已知双曲线$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{3m}$=1的一个焦点为（2，0）．
（1）求双曲线的实轴长和虚轴长；
（2）若M（4，0），点N（x，y）是双曲线上的任意一点，求|MN|的最小值．
7．已知点A（-2，4），B（4，2），直线l过点P（0，-2）与线段AB相交，则直线l的斜率k的取值范围是k≤-3或k≥1．
8．设集合A={x|-1＜x≤5}，B={x|-1＜x＜5}，则A∩B=（　　）
A．{x|-1＜x＜5}B．{x|3＜x＜5}C．{x|-1＜x＜1}D．{x|1＜x＜3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网