题目内容
(16分)已知函数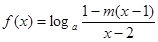 (
(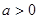 ,
,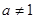 ).
).
(1)若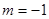 时,判断函数
时,判断函数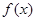 在
在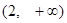 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)若对于定义域内一切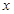 ,
,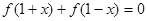 恒成立,求实数
恒成立,求实数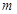 的值;
的值;
(3)在 (2)的条件下,当
(2)的条件下,当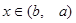 时,
时,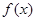 的取值恰为
的取值恰为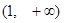 ,求实数
,求实数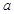 ,
,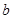 的值.
的值.
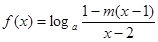 (
(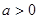 ,
,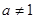 ).
).(1)若
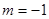 时,判断函数
时,判断函数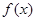 在
在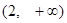 上的单调性,并说明理由;
上的单调性,并说明理由;(2)若对于定义域内一切
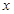 ,
,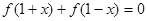 恒成立,求实数
恒成立,求实数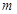 的值;
的值;(3)在
 (2)的条件下,当
(2)的条件下,当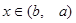 时,
时,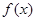 的取值恰为
的取值恰为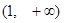 ,求实数
,求实数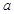 ,
,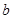 的值.
的值.(1)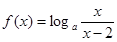 ,任取
,任取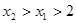 ,记
,记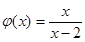 ,
,

 ,
,
 单调递减.
单调递减.
当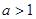 时,
时,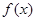 在
在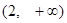 单调递减;
单调递减;
当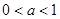 时,
时,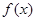 在
在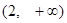 单调递增.…………………………………………4分
单调递增.…………………………………………4分
(2)由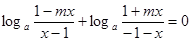 ,得
,得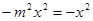 ,
,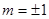 ……………………
…………………… 8分
8分
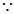 当
当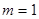 时,
时,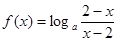 无意义.
无意义.

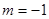 ,
,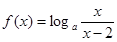 ………………………………………………………10分
………………………………………………………10分
(3)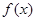 的定义域为
的定义域为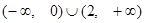
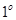 .若
.若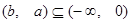 ,与
,与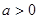 矛盾,不合;………………………………12分
矛盾,不合;………………………………12分
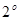 .若
.若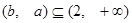 ,
,
 .
.
取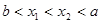 ,
,
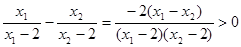 .
.
又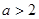 ,
,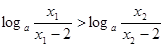 ,此时
,此时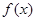 为减函数
为减函数
(或由(1)得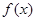 为减函数)…………………………………………………14分
为减函数)…………………………………………………14分
 值域
值域 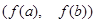 为
为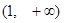 ,
,
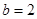 ………………………………15分
………………………………15分
又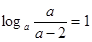 ,得
,得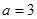 ……………………………………………………16分
……………………………………………………16分
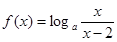 ,任取
,任取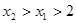 ,记
,记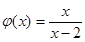 ,
,
 ,
,
 单调递减.
单调递减.当
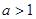 时,
时,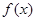 在
在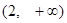 单调递减;
单调递减;当
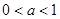 时,
时,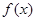 在
在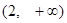 单调递增.…………………………………………4分
单调递增.…………………………………………4分(2)由
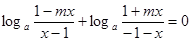 ,得
,得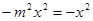 ,
,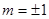 ……………………
…………………… 8分
8分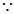 当
当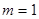 时,
时,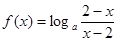 无意义.
无意义.
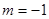 ,
,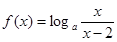 ………………………………………………………10分
………………………………………………………10分(3)
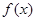 的定义域为
的定义域为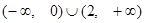
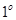 .若
.若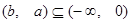 ,与
,与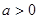 矛盾,不合;………………………………12分
矛盾,不合;………………………………12分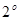 .若
.若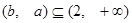 ,
,
 .
.取
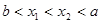 ,
,
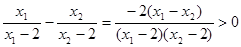 .
.又
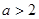 ,
,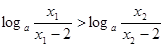 ,此时
,此时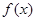 为减函数
为减函数(或由(1)得
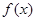 为减函数)…………………………………………………14分
为减函数)…………………………………………………14分 值域
值域 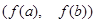 为
为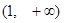 ,
,
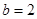 ………………………………15分
………………………………15分又
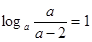 ,得
,得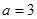 ……………………………………………………16分
……………………………………………………16分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
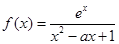 .(其中e为自然对数的底数,e=2.71828…〉.
.(其中e为自然对数的底数,e=2.71828…〉.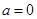 时,求函数
时,求函数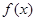 的图
的图 象在点
象在点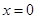 处的切线方程;
处的切线方程;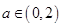 时,试求函数
时,试求函数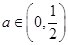 ,则当
,则当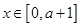 时,函数
时,函数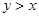 所表示的平面区域内,请写出判
所表示的平面区域内,请写出判 断过程.
断过程.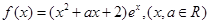 其中
其中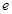 为自然对数的底数
为自然对数的底数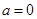 时,求曲线
时,求曲线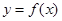 在
在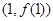 处的切线方程;
处的切线方程;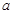 的取值范围;
的取值范围;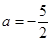 时,求函数
时,求函数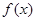 的极小值。
的极小值。 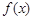 的定义域为开区间
的定义域为开区间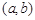 ,导函数
,导函数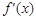 在
在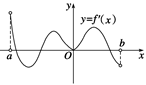
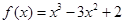 在区间[-1,1]上的极大值是 ( )
在区间[-1,1]上的极大值是 ( )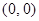 作曲线
作曲线 的切线,则切线方程为________.
的切线,则切线方程为________.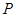 在曲线
在曲线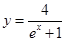 上,
上,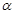 为曲线在点
为曲线在点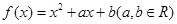 ,若函数在点
,若函数在点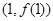 处的切线为
处的切线为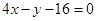 ,数列
,数列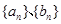 定义:
定义: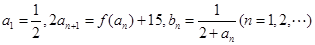 。
。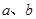 的值;
的值;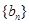 的前
的前 项的和与积分别记为
项的和与积分别记为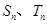 。证明:对任意正整数
。证明:对任意正整数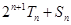 为定值;证明:对任意正整数
为定值;证明:对任意正整数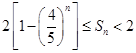 。
。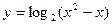 的递增区间是:________________
的递增区间是:________________