题目内容
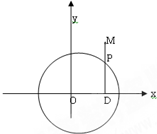
如图，DP⊥x轴，点M在DP的延长线上，且
=
，当点P在圆x2+y2=4上运动时，求：动点M的轨迹方程．
| |DM| |
| |DP| |
| 3 |
| 2 |
设M（x，y），
由
=
，得P（x，
），
又∵点P在圆x2+y2=4上，
∴x2+(
)2=4．
∵D坐标为（x，0），当x=±2时，P点和D点坐标相同，即俩点重合，此时约束条件中DP垂直于x轴没有意义，
故x=±2舍去．
∴M的轨迹方程是：
+
=1(x≠±2)．
由
| |DM| |
| |DP| |
| 3 |
| 2 |
| 2y |
| 3 |
又∵点P在圆x2+y2=4上，
∴x2+(
| 2y |
| 3 |
∵D坐标为（x，0），当x=±2时，P点和D点坐标相同，即俩点重合，此时约束条件中DP垂直于x轴没有意义，
故x=±2舍去．
∴M的轨迹方程是：
| x2 |
| 4 |
| y2 |
| 9 |
练习册系列答案
相关题目
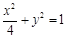上；
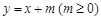与椭圆W：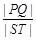
的最大值及取得最大值时m的值．