题目内容
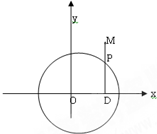
动点在圆x2+y2=1上运动,它与定点B(-2,0)连线的中点的轨迹方程是______.
设动点P(x0,y0),PB的中点为Q(x,y),
可得x=
(-2+x0),y=
y0,解出x0=2x+2,y0=2y,
∵点P(x0,y0)即P(2x+2,2y)在圆x2+y2=1上运动,
∴(2x+2)2+(2y)2=1,化简得(x+1)2+y2=
,即为所求动点轨迹方程
故答案为:(x+1)2+y2=
可得x=
| 1 |
| 2 |
| 1 |
| 2 |
∵点P(x0,y0)即P(2x+2,2y)在圆x2+y2=1上运动,
∴(2x+2)2+(2y)2=1,化简得(x+1)2+y2=
| 1 |
| 4 |
故答案为:(x+1)2+y2=
| 1 |
| 4 |

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
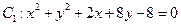 ,圆
,圆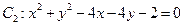 ,
,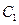 与圆
与圆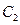 的关系。
的关系。