题目内容
在△ABC中,若sinB、cos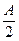 、sinC成等比数列,则此三角形的形状是 三角形。
、sinC成等比数列,则此三角形的形状是 三角形。
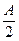 、sinC成等比数列,则此三角形的形状是 三角形。
、sinC成等比数列,则此三角形的形状是 三角形。等腰三角形
易知cos2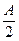 =sinB·sinC,∴1+cosA=2sinBsinC,
=sinB·sinC,∴1+cosA=2sinBsinC,
即1-cos(B+C)=2sinBsinC,即1-cosBcosC+sinBsinC=2sinBsinC.
∴1-cosBcosC="sinB" sinC.∴cos(B-C)=1.
∵0<B<π,0<C<π,∴-π<B-C<π,∴B-C=0,B=C.∴△ABC为等腰三角形.
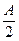 =sinB·sinC,∴1+cosA=2sinBsinC,
=sinB·sinC,∴1+cosA=2sinBsinC,即1-cos(B+C)=2sinBsinC,即1-cosBcosC+sinBsinC=2sinBsinC.
∴1-cosBcosC="sinB" sinC.∴cos(B-C)=1.
∵0<B<π,0<C<π,∴-π<B-C<π,∴B-C=0,B=C.∴△ABC为等腰三角形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
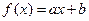 ,当
,当 时,值域为
时,值域为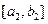 ,当
,当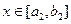 时,值域为
时,值域为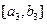 ,…,当
,…,当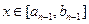 时,值域为
时,值域为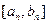 ,….其中a、b为常数,a1=0,b1=1.
,….其中a、b为常数,a1=0,b1=1.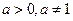 ,要使数列{bn}是公比不为1的等比数列,求b的值
,要使数列{bn}是公比不为1的等比数列,求b的值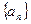 中,
中,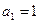 ,
,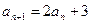 ,则
,则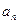 = .
= .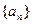 满足:
满足: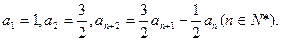
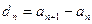 ,求证:{dn}是等比数列;
,求证:{dn}是等比数列;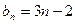 ,求数列
,求数列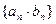 的前n项和Sn。
的前n项和Sn。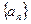 的前n项和为Sn,S4=1,S8=17,求通项公式an.
的前n项和为Sn,S4=1,S8=17,求通项公式an.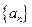 中,
中,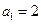 ,前
,前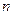 项和为
项和为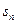 ,若数列
,若数列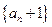 也是等比数列,则
也是等比数列,则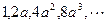 的前
的前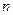 项和Sn= .
项和Sn= .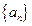 中,已知
中,已知 ,这个数列的通项公式是_______________;
,这个数列的通项公式是_______________;