题目内容
.已知函数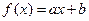 ,当
,当 时,值域为
时,值域为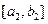 ,当
,当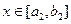 时,值域为
时,值域为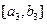 ,…,当
,…,当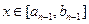 时,值域为
时,值域为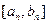 ,….其中a、b为常数,a1=0,b1=1.
,….其中a、b为常数,a1=0,b1=1.
(1)若a=1,求数列{an}与数列{bn}的通项公式;
(2)若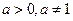 ,要使数列{bn}是公比不为1的等比数列,求b的值
,要使数列{bn}是公比不为1的等比数列,求b的值
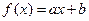 ,当
,当 时,值域为
时,值域为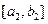 ,当
,当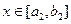 时,值域为
时,值域为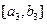 ,…,当
,…,当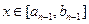 时,值域为
时,值域为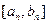 ,….其中a、b为常数,a1=0,b1=1.
,….其中a、b为常数,a1=0,b1=1.(1)若a=1,求数列{an}与数列{bn}的通项公式;
(2)若
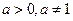 ,要使数列{bn}是公比不为1的等比数列,求b的值
,要使数列{bn}是公比不为1的等比数列,求b的值⑴∵a=1>0,∴f(x)=ax+b在R上为增函数,
∴an=a·an-1+b=an-1+b,bn=bn-1+b(n≥2),
∴数列{an},{bn}都是公差为b的等差数列.
又a1=0,b1=1,∴an=(n-1)b,bn=1+(n-1)b(n≥2)
⑵∵a>0,bn=abn-1+b,∴,
由{bn}是等比数列知为常数.又∵{bn}是公比不为1的等比数列,则bn-1不为常数,
∴必有b=0.
∴an=a·an-1+b=an-1+b,bn=bn-1+b(n≥2),
∴数列{an},{bn}都是公差为b的等差数列.
又a1=0,b1=1,∴an=(n-1)b,bn=1+(n-1)b(n≥2)
⑵∵a>0,bn=abn-1+b,∴,
由{bn}是等比数列知为常数.又∵{bn}是公比不为1的等比数列,则bn-1不为常数,
∴必有b=0.
同答案

练习册系列答案
相关题目
 中,
中,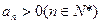 ,公比
,公比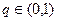 ,且
,且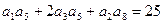 ,又
,又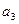 与
与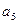 的等比中项为
的等比中项为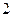 ,
,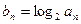 ,数列
,数列 的前
的前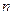 项和为
项和为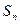 。
。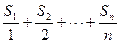 最大值?
最大值?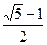 <r<
<r<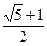 B.0<r<
B.0<r<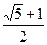
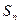 为数列
为数列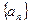 的前
的前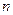 项和,
项和,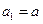 ,
,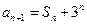 ,
,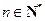 .
.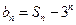 ,求数列
,求数列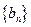 的通项公式;
的通项公式;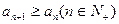 ,求
,求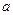 的取值范围.
的取值范围.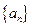 的前
的前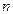 项和为
项和为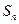 ,
,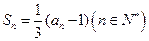 ;
;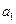 ,
,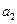 的值;
的值; 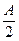 、sinC成等比数列,则此三角形的形状是 三角形。
、sinC成等比数列,则此三角形的形状是 三角形。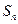 为等比数列
为等比数列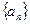 的前
的前 项和,
项和,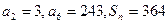 ,则
,则 ;
;