题目内容
已知函数 ,
,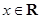 .
.
(1)求 的值及函数
的值及函数 的最小正周期;
的最小正周期;
(2)求函数 在
在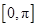 上的单调减区间.
上的单调减区间.
(1)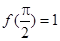 ,函数
,函数 的最小正周期为
的最小正周期为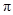 ;(2)函数
;(2)函数 在
在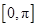 上的单调减区间为
上的单调减区间为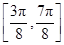 .
.
解析试题分析:(1)求 的值及函数
的值及函数 的最小正周期,首先对函数
的最小正周期,首先对函数 进行化简,将他化为一个角的一个三角函数,由已知
进行化简,将他化为一个角的一个三角函数,由已知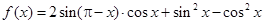 ,可用诱导公式及二倍角公式将函数
,可用诱导公式及二倍角公式将函数 化为
化为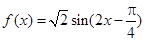 ,即可求出
,即可求出 的值及函数
的值及函数 的最小正周期;(2)求函数
的最小正周期;(2)求函数 在
在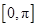 上的单调减区间,由(1)知
上的单调减区间,由(1)知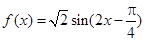 ,可利用
,可利用 的单调递减区间得,
的单调递减区间得,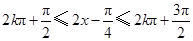 ,
,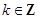 ,解出
,解出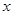 ,即得
,即得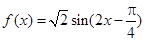 的单调递减区间得,从而得函数
的单调递减区间得,从而得函数 在
在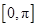 上的单调减区间.
上的单调减区间.
试题解析: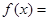
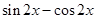
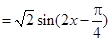 .
.
(1)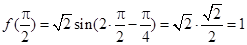 .
.
显然,函数 的最小正周期为
的最小正周期为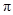 . 8分
. 8分
(2)令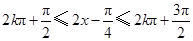 得
得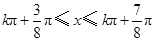 ,
,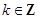 .
.
又因为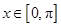 ,所以
,所以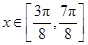 .
.
函数 在
在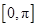 上的单调减区间为
上的单调减区间为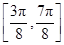 . 13分
. 13分
考点:三角函数化简,倍角公式,周期,单调性.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
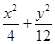 =1上在第一象限的点,A(2,0),B(0,2
=1上在第一象限的点,A(2,0),B(0,2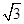 )
) ,且
,且 ,求
,求 的值。
的值。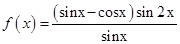 .
.  的定义域及最小正周期;
的定义域及最小正周期; )的部分图象如图所示.
)的部分图象如图所示.
 的单调递增区间.
的单调递增区间.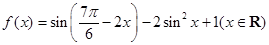 ,
,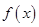 的周期及单调递增区间;
的周期及单调递增区间;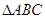 中,三内角
中,三内角 ,
,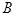 ,
, 的对边分别为
的对边分别为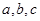 ,已知函数
,已知函数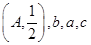 成等差数列,且
成等差数列,且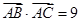 ,求
,求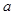 的值.
的值.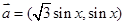 ,
,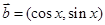 ,
,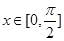
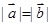 ,求
,求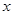 的值;
的值;  ,求
,求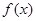 的最大值。
的最大值。 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)图象的一个对称中心到最近的对称轴的距离为 .
. ]上的最大值和最小值.
]上的最大值和最小值. .
.