题目内容
已知函数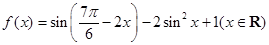 ,
,
(1)求函数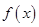 的周期及单调递增区间;
的周期及单调递增区间;
(2)在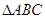 中,三内角
中,三内角 ,
,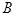 ,
, 的对边分别为
的对边分别为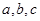 ,已知函数
,已知函数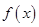 的图象经过点
的图象经过点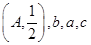 成等差数列,且
成等差数列,且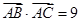 ,求
,求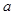 的值.
的值.
(1)最小正周期: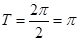 ,递增区间为:
,递增区间为: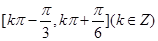 ;
;
(2)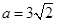 .
.
解析试题分析:首先应用和差倍半的三角函数公式,化简得到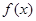
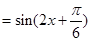
(1)最小正周期: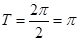 ,利用“复合函数的单调性”,求得
,利用“复合函数的单调性”,求得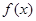 的单调递增区间
的单调递增区间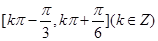 ;
;
(2)由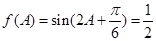 及
及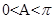 可得
可得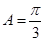 ,
,
根据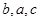 成等差数列,得
成等差数列,得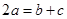 ,
,
根据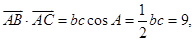 得
得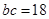 ,应用余弦定理即得所求.
,应用余弦定理即得所求.
试题解析: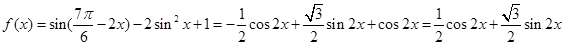
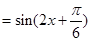 3分
3分
(1)最小正周期: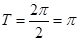 , 4分
, 4分
由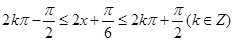 可解得:
可解得: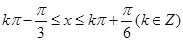 ,
,
所以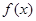 的单调递增区间为:
的单调递增区间为: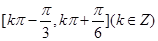 ; 6分
; 6分
(2)由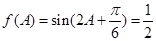 可得:
可得: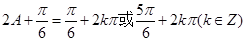
所以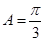 , 8分
, 8分
又因为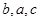 成等差数列,所以
成等差数列,所以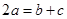 , 9分
, 9分
而 10分
10分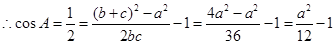 ,
,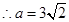 . 12分
. 12分
考点:等差数列,和差倍半的三角函数,余弦定理的应用,三角函数的性质,平面向量的数量积.

练习册系列答案
相关题目
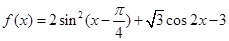 ,
,
 的最大值和最小值;
的最大值和最小值;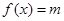 仅有一解,求实数
仅有一解,求实数 的取值范围.
的取值范围.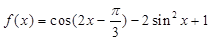 .
. 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值. ,钝角
,钝角 (角
(角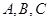 对边为
对边为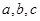 )的角
)的角 满足
满足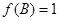 .
.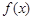 的单调递增区间;
的单调递增区间;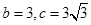 ,求
,求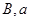 .
. ,
,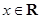 .
. 的值及函数
的值及函数 的最小正周期;
的最小正周期;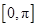 上的单调减区间.
上的单调减区间. 为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径
为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径 ,
, ,
, 与
与 之间的夹角为
之间的夹角为 .
.
 的面积
的面积 表示成
表示成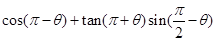 .
. sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为 ,且点
,且点 是它的一个对称中心.
是它的一个对称中心.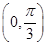 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.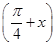 sin
sin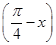 +
+ sinxcosx(x∈R).
sinxcosx(x∈R).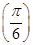 的值;
的值;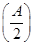 =1,求sinB+sinC的最大值.
=1,求sinB+sinC的最大值.