题目内容
(已知椭圆
 经过点
经过点 其离心率为
其离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点.求
为坐标原点.求 到直线
到直线 距离的最小值.
距离的最小值.
(Ⅰ)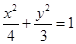 ;(Ⅱ)
;(Ⅱ)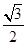
解析试题分析:(Ⅰ)由离心率为 ,得
,得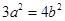 ①,又过点
①,又过点 ,得
,得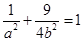 ②,联立①②求
②,联立①②求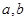 ;
;
(Ⅱ)直线和圆锥曲线的位置关系问题,一般会根据已知条件结合韦达定理列式确定参数的值或者取值范围,设直线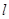 :
: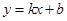 ,联立椭圆方程,消去
,联立椭圆方程,消去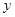 ,得关于
,得关于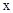 的二次方程,设
的二次方程,设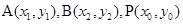 ,利用韦达定理将点
,利用韦达定理将点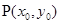 的坐标表示出来,
的坐标表示出来, ,因为
,因为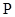 在椭圆
在椭圆 上,代入椭圆方程,得
上,代入椭圆方程,得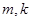 的等式①,点
的等式①,点 到直线
到直线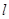 的距离为
的距离为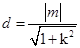 ,联立①得关于
,联立①得关于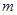 ,或
,或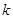 的函数,进而求其最小值,再考虑斜率不存在时的情况,求最小值,然后和斜率存在时候的最小值比较大小,得结论.
的函数,进而求其最小值,再考虑斜率不存在时的情况,求最小值,然后和斜率存在时候的最小值比较大小,得结论.
试题解析:(Ⅰ)由已知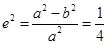 ,所以
,所以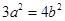 , ① 又点
, ① 又点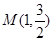 在椭圆
在椭圆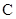 上,所以
上,所以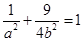 , ② 由①②解之得
, ② 由①②解之得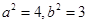 ,故椭圆
,故椭圆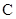 的方程为
的方程为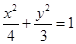 ;
;
(Ⅱ)当直线 有斜率时,设
有斜率时,设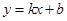 时,则由
时,则由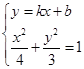
消去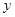 得
得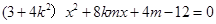 ,
,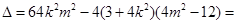
 , ③
, ③
设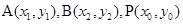 则
则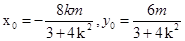 ,由于点
,由于点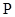 在椭圆
在椭圆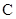 上,所以
上,所以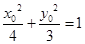 ,从而
,从而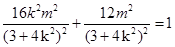 ,化简得
,化简得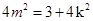 ,经检验满足③式,又点
,经检验满足③式,又点 到直线
到直线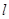 的距离为:
的距离为: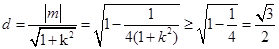 ,并且仅当
,并且仅当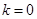 时等号成立;当直线
时等号成立;当直线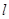 无斜率时,由对称性知,点
无斜率时,由对称性知,点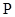 一定在
一定在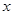 轴上,从而
轴上,从而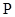 点为
点为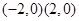 ,直线
,直线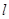 为
为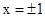 ,所以点
,所以点 到直线
到直线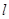 的距离为1,所以点
的距离为1,所以点 到直线
到直线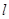 的距离最小值为
的距离最小值为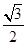 .
.
考点:1、椭圆的标准方程;2、韦达定理;3、点到直线的距离.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 的顶点
的顶点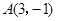 ,过点
,过点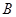 的内角平分线所在直线方程是
的内角平分线所在直线方程是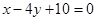 ,过点C的中线所在直线的方程是
,过点C的中线所在直线的方程是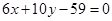
 的顶点A为(3,-1),AB边上的中线所在直线方程为
的顶点A为(3,-1),AB边上的中线所在直线方程为 ,
, 的平分线所在直线方程为
的平分线所在直线方程为 ,求BC边所在直线的方程.
,求BC边所在直线的方程. 过点P(2,1),夹在两已知直线
过点P(2,1),夹在两已知直线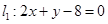 和
和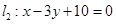 之间的线段AB恰被点P平分.
之间的线段AB恰被点P平分.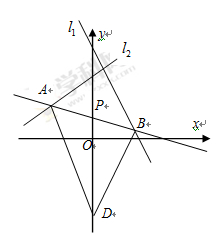
 的方程;
的方程; ,求:
,求: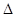 ABD的面积.
ABD的面积. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程.
为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程. ,
,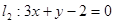 相交于
相交于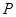 点.
点.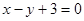 垂直的直线
垂直的直线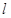 的方程.
的方程. 和
和 的交点,且平行于直线
的交点,且平行于直线 ;
;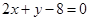 和
和 的交点,且垂直于直线
的交点,且垂直于直线 .
. :
:
 取何值,直线
取何值,直线