题目内容
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程.
为参数),若以直角坐标系xoy的原点为极点,OX为极轴,且长度单位相同,建立极坐标系,直线l的极坐标方程为 ρsin(θ+)="0," 求与直线l垂直且与曲线C相切的直线m的极坐标方程.
 或
或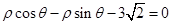 .
.
解析试题分析:将直线和圆的方程化为直角坐标系下的方程,设 ,利用直线和圆相切求出直线
,利用直线和圆相切求出直线 ,再将方程化为极坐标方程.
,再将方程化为极坐标方程.
试题解析: 3分
3分
设 ,
, 直线
直线 与
与 相切,可得
相切,可得 或
或 , 7分
, 7分 直线
直线 的极坐标方程为
的极坐标方程为 或
或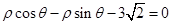 10分
10分
考点:极坐标和直角坐标方程的互化、点到直线的距离公式.

练习册系列答案
相关题目
 ,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程.
,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程. 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程:
 经过点
经过点 其离心率为
其离心率为 .
.  的方程;
的方程; 与椭圆
与椭圆 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 为坐标原点.求
为坐标原点.求 的顶点
的顶点 的坐标为
的坐标为 ,
, 边上的中线所在直线方程为
边上的中线所在直线方程为 的平分线所在直线方程为
的平分线所在直线方程为 ,求
,求 边所在直线的方程。
边所在直线的方程。 ,点
,点 分别为圆锥曲线C的左、右焦点,点B为圆锥曲线C的上顶点,求经过点
分别为圆锥曲线C的左、右焦点,点B为圆锥曲线C的上顶点,求经过点 且垂直于直线
且垂直于直线 的直线
的直线 的方程.
的方程. 的方程为3x+4y-12=0,求满足下列条件的直线
的方程为3x+4y-12=0,求满足下列条件的直线 的方程.
的方程.

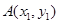 ,
, 是抛物线
是抛物线 上相异两点,且满足
上相异两点,且满足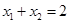 .
. 的中垂线经过点
的中垂线经过点 ,求直线
,求直线 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线