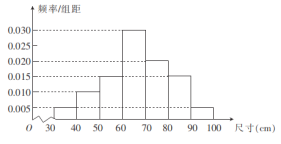
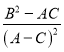��Ŀ����
����Ŀ����֪��Բ![]() ��a��b��0�������������ΪA��B�����ҽ���ֱ�ΪF1��F2������Ϊ2c��a=2c����F1�Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊ3��
��a��b��0�������������ΪA��B�����ҽ���ֱ�ΪF1��F2������Ϊ2c��a=2c����F1�Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊ3��
��1������ԲC�ķ��̣�
��2����˫����![]() ��ȡ��Q�����ڶ��㣩��ֱ��OQ����ԲC���ڵ�P����ֱ��AP��BP��AQ��BQ��б�ʷֱ�Ϊk1��k2��k3��k4����֤����k1+k2+k3+k4Ϊ��ֵ��
��ȡ��Q�����ڶ��㣩��ֱ��OQ����ԲC���ڵ�P����ֱ��AP��BP��AQ��BQ��б�ʷֱ�Ϊk1��k2��k3��k4����֤����k1+k2+k3+k4Ϊ��ֵ��
��3������ԲC���������K��y2=4x��ȡһ��E����EF1��EF2��б�ʷֱ�Ϊ![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1��![]() ��2��0��3��
��2��0��3��![]()
��������
��1������Բ��ͨ����ʽ��a=2c���������a��b��ֵ�����������Բ���̷��̣�
��2������ֱ�ߵ�б�ʹ�ʽ�����![]() ��
�� ![]() ����
����![]() ���ߣ���
���ߣ���![]()
![]() ��������ý��ۣ�
��������ý��ۣ�
��3������E�������ʾ![]() ���ٸ��ݺ��������Լ������
���ٸ��ݺ��������Լ������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��1��������a=2c����Բ��ͨ��Ϊ![]() =3��
=3��
��Ϊa2=b2+c2������a=2��b=![]() ��c=1��
��c=1��
����Բ�ı����̣�![]() ��
��
��2���ɣ�1����֪��A����2��0����B��2��0����F1����1��0����F2��1��0������P��x1��y1����
��![]() ����
����![]()
![]() =
=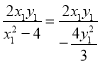
![]()
![]()
��Q��x2��y2������![]() ����
����
��![]()
![]() =
=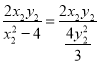 =
=![]() ��
��
��![]() ���ߣ���
���ߣ���![]() ��
��![]()
��3����![]() ����
����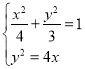 ����ã�
����ã�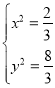 ��
��
��E����ԲC���������K��y2=4x��һ�㣬��![]() ��
��
��EF1 ��EF2��б�ʷֱ�Ϊ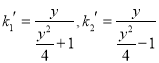 ����
����![]() ��
��![]()
��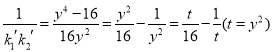 ����
����![]() ��
��
�ڣ�![]() ��4������4��+�����Ϸֱ�������
��4������4��+�����Ϸֱ�������
��![]() ��ȡֵ��Χ
��ȡֵ��Χ![]() ��
��