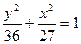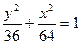题目内容
已知圆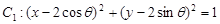 与圆
与圆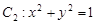 ,在下列说法中:
,在下列说法中:
①对于任意的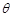 ,圆
,圆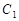 与圆
与圆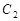 始终相切;
始终相切;
②对于任意的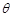 ,圆
,圆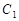 与圆
与圆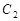 始终有四条公切线;
始终有四条公切线;
③当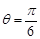 时,圆
时,圆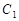 被直线
被直线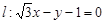 截得的弦长为
截得的弦长为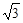 ;
;
④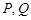 分别为圆
分别为圆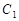 与圆
与圆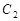 上的动点,则
上的动点,则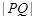 的最大值为4.
的最大值为4.
其中正确命题的序号为______.
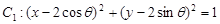 与圆
与圆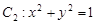 ,在下列说法中:
,在下列说法中:①对于任意的
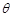 ,圆
,圆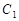 与圆
与圆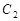 始终相切;
始终相切;②对于任意的
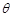 ,圆
,圆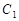 与圆
与圆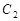 始终有四条公切线;
始终有四条公切线;③当
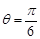 时,圆
时,圆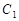 被直线
被直线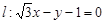 截得的弦长为
截得的弦长为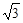 ;
;④
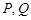 分别为圆
分别为圆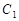 与圆
与圆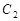 上的动点,则
上的动点,则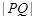 的最大值为4.
的最大值为4.其中正确命题的序号为______.
①③④
对于①,我们知道两个圆相切等价于两个圆的圆心距刚好等于两个圆的半径之和,有题意,有:圆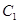 的半径为:1,圆心为:
的半径为:1,圆心为: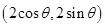 ;圆
;圆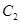 的半径为:1,圆心为:
的半径为:1,圆心为: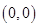 ,所以两个圆的圆心距为:
,所以两个圆的圆心距为: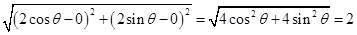 ,又因为,两圆的半径之和为:1+1=2=圆心距,所以对于任意
,又因为,两圆的半径之和为:1+1=2=圆心距,所以对于任意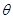 ,圆
,圆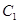 和圆
和圆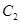 始终相切。
始终相切。
对于②,从①有,两圆相切,所以两圆只有三条公切线,所以②错误。
对于③,我们有圆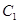 的方程为:
的方程为: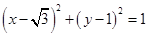 ,故有圆
,故有圆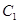 的圆心为:
的圆心为: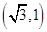 ,设其被
,设其被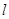 所截弦为
所截弦为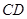 ,过圆心
,过圆心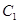 做
做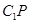 垂直于
垂直于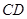 ,则由圆的性质,有
,则由圆的性质,有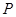 是弦
是弦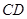 的中点,所以圆心到直线
的中点,所以圆心到直线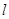 的距离为:
的距离为: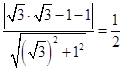 ,又因为圆
,又因为圆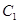 的半径为1,所以有其所截弦
的半径为1,所以有其所截弦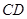 的长为:
的长为: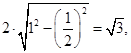 所以③正确。
所以③正确。
对于④,由①有,两圆相切,所以两圆上的点的最大距离就是两圆的直径之和,因为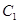 的直径为2,
的直径为2,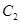 的直径也为2,也就是说
的直径也为2,也就是说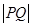 的最大值为:2+2=4.
的最大值为:2+2=4.
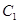 的半径为:1,圆心为:
的半径为:1,圆心为: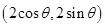 ;圆
;圆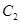 的半径为:1,圆心为:
的半径为:1,圆心为: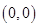 ,所以两个圆的圆心距为:
,所以两个圆的圆心距为: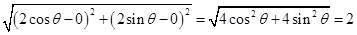 ,又因为,两圆的半径之和为:1+1=2=圆心距,所以对于任意
,又因为,两圆的半径之和为:1+1=2=圆心距,所以对于任意 ,圆
,圆 和圆
和圆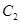 始终相切。
始终相切。对于②,从①有,两圆相切,所以两圆只有三条公切线,所以②错误。
对于③,我们有圆
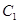 的方程为:
的方程为: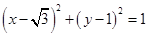 ,故有圆
,故有圆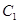 的圆心为:
的圆心为: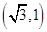 ,设其被
,设其被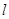 所截弦为
所截弦为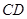 ,过圆心
,过圆心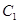 做
做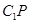 垂直于
垂直于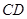 ,则由圆的性质,有
,则由圆的性质,有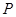 是弦
是弦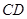 的中点,所以圆心到直线
的中点,所以圆心到直线 的距离为:
的距离为: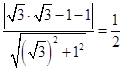 ,又因为圆
,又因为圆 的半径为1,所以有其所截弦
的半径为1,所以有其所截弦 的长为:
的长为: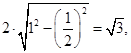 所以③正确。
所以③正确。对于④,由①有,两圆相切,所以两圆上的点的最大距离就是两圆的直径之和,因为
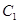 的直径为2,
的直径为2,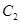 的直径也为2,也就是说
的直径也为2,也就是说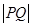 的最大值为:2+2=4.
的最大值为:2+2=4.
练习册系列答案
相关题目
 与
与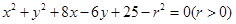 相交,则
相交,则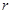 的取值范围是 ▲ .
的取值范围是 ▲ .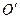 相交于A,B两点,AC是圆
相交于A,B两点,AC是圆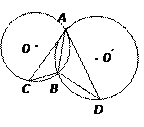 是圆O的切线,若BC=2,AB=4,求BD.
是圆O的切线,若BC=2,AB=4,求BD.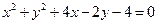 ,则
,则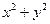 的最大值是 .
的最大值是 .
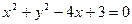 和
和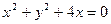 都外切,则动圆圆心的轨迹为( )
都外切,则动圆圆心的轨迹为( )
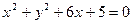 外切,同时与圆
外切,同时与圆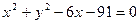 内切,则动圆圆心的轨迹方程是[
内切,则动圆圆心的轨迹方程是[