Question

【题目】已知椭圆C： 的右焦点为F，不垂直x轴且不过F点的直线l与椭圆C相交于A，B两点．
（Ⅰ）若直线l经过点P（2，0），则直线FA、FB的斜率之和是否为定值？若是，求出该定值；若不是，请说明理由；
（Ⅱ）如果FA⊥FB，原点到直线l的距离为d，求d的取值范围．

Answer 1

【答案】解：（I）直线l的方程为y=k（x﹣2），
联立方程组 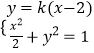，消元得（1+2k2）x2﹣8k2x+8k2﹣2=0，
设A（x1 ， y1），B（x2 ， y2），则x1+x2= ，x1x2= ，
又F（1，0），∴kFA= = ，kFB= = ，
∴kFA+kFB= + = ，
又2kx1x2﹣3k（x1+x2）+4k=2k ﹣3k +4k= =0，
∴kFA+kFB=0，
即直线FA、FB的斜率之和是定值0．
（II）设直线l的方程为y=kx+b，
联立方程组 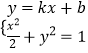，消去y得（1+2k2）x2+4kbx+2（b2﹣1）=0，
∴△=16k2b2﹣8（1+2k2）（b2﹣1）=8（2k2+1﹣b2）＞0，
设A（x3 ， y3），B（x4 ， y4），则x3+x4= ，x3x4= ，
∴kFA= = ，kFB= = ，
若FA⊥FB，则 =﹣1，
即（k2+1）x3x4+（kb﹣1）（x3+x4）+b2+1=0，
∴（k2+1） +（kb﹣1） +b2+1=0，
化简得3b2+4kb﹣1=0，即k= ，
代入判别式得△=b4+2b2+1＞0恒成立，
∴d= = = ，
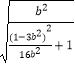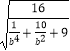∵ + +9＞9，
∴d＜ = ．
∴d的取值范围是（0，9）
【解析】（I）联立方程组，根据根与系数的关系得出A，B两点坐标的关系，表示出直线AF，BF的斜率，计算斜率之和作出判断；（II）设直线l的方程为y=kx+b，联立方程组，根据根与系数的关系得出A，B两点坐标的关系，表示出直线AF，BF的斜率，令斜率之积为﹣1得出k，b的关系，代入距离公式得出d与b的关系，根据判别式得出b的范围，从而得出d的范围．