题目内容
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|,a∈R.
(Ⅰ)若不等式f(x)≥2﹣|x﹣1|恒成立,求实数a的取值范围;
(Ⅱ)当a=1时,直线y=m与函数f(x)的图象围成三角形,求m的最大值及此时围成的三角形的面积.
【答案】解:(I)∵f(x)≥2﹣|x﹣1|恒成立,即|x﹣ ![]() |+|x﹣1|≥1恒成立, 又|x﹣
|+|x﹣1|≥1恒成立, 又|x﹣ ![]() |+|x﹣1|≥|x﹣
|+|x﹣1|≥|x﹣ ![]() ﹣(x﹣1)|=|1﹣
﹣(x﹣1)|=|1﹣ ![]() |,
|,
∴|1﹣ ![]() |≥1,解得a≤0或a≥4.
|≥1,解得a≤0或a≥4.
∴a的取值范围是(﹣∞,0]∪[4,+∞).
(II)当a=1时,f(x)=|2x﹣1|+|x﹣1|= 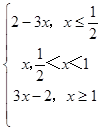 ,
,
做出f(x)的函数图象如图所示: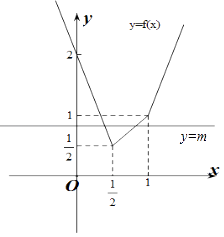
由图象可知当 ![]() <m≤1时,直线y=m与f(x)的图象构成三角形.
<m≤1时,直线y=m与f(x)的图象构成三角形.
∴m的最大值为1,
令2﹣3x=1得x= ![]() ,此时围成三角形的面积为
,此时围成三角形的面积为 ![]() (1﹣
(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]()
【解析】(I)利用绝对值三角不等式得出|x﹣ ![]() |+|x﹣1|的最小值,从而解出a的范围;(II)做出f(x)的函数图象,根据函数图象得出m的范围.
|+|x﹣1|的最小值,从而解出a的范围;(II)做出f(x)的函数图象,根据函数图象得出m的范围.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目