题目内容
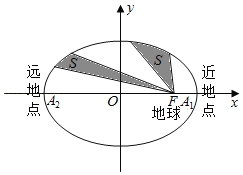
【题目】人造地球卫星绕地球运行遵循开普勒行星运动定律:如图，卫星在以地球的中心为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径(卫星与地心的连线)在相同的时间内扫过的面积相等设该椭圆的长轴长、焦距分别为
，
.某同学根据所学知识，得到下列结论:
①卫星向径的取值范围是
②卫星向径的最小值与最大值的比值越大，椭圆轨道越扁
③卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间
④卫星运行速度在近地点时最小，在远地点时最大
其中正确的结论是（ ）
A.①②B.①③C.②④D.①③④
【答案】B
【解析】
①根据椭圆的简单几何性质可知卫星向径的最小值和最大值分别为什么；
②根据向径的最小值与最大值的比值，结合椭圆的性质即可得出结论；
③根据在相同的时间内扫过的面积相等，即可判断
④根据题意结合椭圆的图形知卫星运行速度在近地点时最大，在远地点时最小．
解：如图所示，
对于①，卫星向径的最小值为
，最大值为
，
①正确；
对于②，卫星向径的最小值与最大值的比值为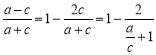
，
越小，
就越大，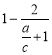
就越小，椭圆轨道越扁，②错误；
对于③，根据在相同的时间内扫过的面积相等，卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间，③正确；
对于④，卫星运行速度在近地点时最大，在远地点时最小，④错误；
综上，正确结论的序号是①③，共2个．
故选
．
练习册系列答案
优加精卷系列答案
相关题目
