题目内容
已知A，B，C是平面上不共线的三点，o为平面ABC内任一点，动点P满足等式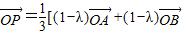
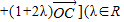且λ≠1，则P的轨迹一定通过△ABC的（ ）A．内心
B．垂心
C．重心
D．外心
【答案】分析：根据向量的加法的平行四边形法则向量的运算法则，取AB的中点D，对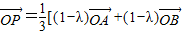
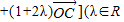，进行化简，得到
=
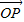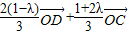，根据三点共线的充要条件知道P、C、D三点共线，从而得到点P的轨迹一定经过△ABC的重心．
解答：解：取AB的中点D，则 2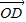
=
，
∵
，
∴
=
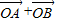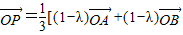
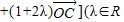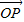[（1-λ）（2
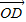）+（1+2λ） 
]
=
，
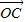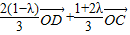而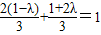
，
∴P、C、D三点共线，
∴点P的轨迹一定经过△ABC的重心．
故选C．
点评：本小题主要考查向量在几何中的应用、三点共线的充要条件的应用、三角形五心等基础知识，考查运算求解能力，考查数形结合思与转化思想．属于基础题．
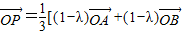
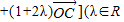，进行化简，得到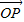=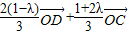，根据三点共线的充要条件知道P、C、D三点共线，从而得到点P的轨迹一定经过△ABC的重心．解答：解：取AB的中点D，则 2
=，∵
，∴
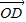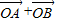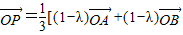
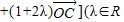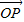=[（1-λ）（2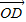）+（1+2λ） ]=
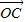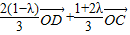，而
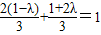，∴P、C、D三点共线，
∴点P的轨迹一定经过△ABC的重心．
故选C．
点评：本小题主要考查向量在几何中的应用、三点共线的充要条件的应用、三角形五心等基础知识，考查运算求解能力，考查数形结合思与转化思想．属于基础题．
练习册系列答案
相关题目
已知A、B、C是平面内不共线的三点，P为平面内的动点，且
=
+λ(
+
) (λ＞0)，则P的轨迹过△ABC的（ ）
| OP |
| ||||
| 2 |
| ||
|
|
| ||
|
|
| A、重心 | B、垂心 | C、内心 | D、外心 |
已知A、B、C是平面上不共线的三点，O是三角形ABC的重心，动点P满足
=
(
+
+2
)，则点P一定为三角形ABC的（ ）
| OP |
| 1 |
| 3 |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| OC |
| A、AB边中线的中点 |
| B、AB边中线的三等分点（非重心） |
| C、重心 |
| D、AB边的中点 |