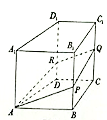
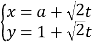��Ŀ����
����Ŀ��������֮�����̴�Ϊ���ҹ�����ΰ����ѧ�ң�����Ӧ����ѧ�������㷨ͳ�ۡ�����������־���ҹ����㷨�ɳ��㵽����ת�����ɣ��̴�λ�ڡ��㷨ͳ�ۡ��г���ʫ�����ʽ������ѧ���⣬������һ�ס���Ͳ���ס����⣺�����оŽ���һ����Ϊ��ʢ�ײ���ƽ����ͷ���������ţ������Ľڴ�������Ψ���м�������Ҫ�������ε�ʢ�������������㷨��Ҳ����õ�����������ע�������ţ�![]() �����ε�ʢ��ʢ���ݻ��������ͬһ����.��������ѧ����ѧ֪ʶ����м����ڵ��ݻ�Ϊ�� ��
�����ε�ʢ��ʢ���ݻ��������ͬһ����.��������ѧ����ѧ֪ʶ����м����ڵ��ݻ�Ϊ�� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
���𰸡�B
��������
������ͬһ����Ϊ![]() �����¶˵�һ��ʢ��
�����¶˵�һ��ʢ��![]() ������������ó�����
���������������![]() ��
��![]() �ķ����飬�������������ֵ�����ɼ�����м�����ʢ���ݻ�
�ķ����飬�������������ֵ�����ɼ�����м�����ʢ���ݻ�![]() ��.
��.
Ҫ������ʢ���ݻ����ͬһ�����ķ�ʽʢ�ף�
������ͬһ����Ϊ![]() �����¶˵�һ��ʢ��
�����¶˵�һ��ʢ��![]() ����
����
������� �����
�����![]() ��
��
���ԣ��м�����ʢ���ݻ�Ϊ![]() ��������
��������
��ѡ��B.

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ