题目内容
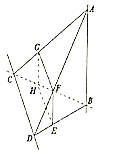
【题目】如图，在四棱柱
中，
平面
，
，
，
，
为棱
上一动点，过直线
的平面分别与棱
，
交于点
，
，则下列结论正确的是__________．
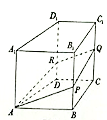
①对于任意的点，都有
②对于任意的点，四边形
不可能为平行四边形
③存在点，使得
为等腰直角三角形
④存在点，使得直线
平面
【答案】①②④
【解析】分析：根据面面平行的性质判断A，B，使用假设法判断C，D．
详解：（1）∵AB∥CD，AA1∥DD1，
∴平面ABB1A1∥平面CDD1C1，∵平面APQR∩平面ABB1A1=AP，平面APQR∩平面CDD1C1=RQ，
∴AP∥QR，故A正确．
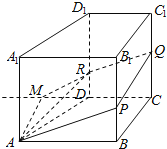
（2）∵四边形ABCD是直角梯形，AB∥CD，∴平面BCC1B1与平面ADD1A1不平行，
∵平面APQR∩平面BCC1B1=PQ，平面APQR∩平面ADD1A1=AR，
∴PQ与AR不平行，故四边形APQR不可能为平行四边形，故B正确．
（3）延长CD至M，使得DM=CM，则四边形ABCM是矩形，∴BC∥AM．
当R，Q，M三点共线时，AM平面APQR，∴BC∥平面APQR，故D正确．
故答案为：①②④．
练习册系列答案
相关题目
