题目内容
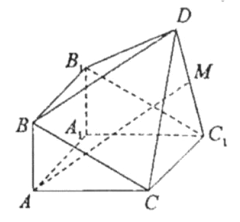
【题目】如图，在正方体
中，平面
与正方体的各个面所在的平面所成的二面角的大小分别是多少？
【答案】平面
与平面ABCD，平面
，平面
，平面
都成45°，平面
与平面
，平面
成的角为90°
【解析】
根据线面垂直判定面面垂直得二面角为90°，根据二面角定义找出二面角的平面角，并求出大小.
解：在正方体
中，考虑平面与平面ABCD，
平面
，
平面，所以平面
就是平面与平面ABCD所成角，
即平面与平面ABCD成角
，
同理平面与平面ABCD，平面，平面，平面都成45°角，
又因为平面，平面与平面垂直，即所成的角为90°，同理可得平面与平面，平面都垂直，即与它们所成的角为90°.
所以平面与平面ABCD，平面，平面，平面都成45°角，平面与平面，平面都垂直，即与它们所成的角为90°.
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
【题目】十九大提出，加快水污染防治，建设美丽中国
根据环保部门对某河流的每年污水排放量
单位：吨
的历史统计数据，得到如下频率分布表：
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立．
（Ⅰ）求在未来3年里，至1年污水排放量
的概率；
（Ⅱ）该河流的污水排放对沿河的经济影响如下：当
时，没有影响；当时，经济损失为10万元；当
时，经济损失为60万元为减少损失，现有三种应对方案：
方案一：防治350吨的污水排放，每年需要防治费
万元；
方案二：防治310吨的污水排放，每年需要防治费2万元；
方案三：不采取措施．
试比较上述三种方案，哪种方案好，并请说明理由．
