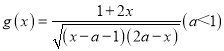题目内容
【题目】已知抛物线![]() 的焦点
的焦点![]() 与椭圆
与椭圆![]() 的右焦点重合,抛物线
的右焦点重合,抛物线![]() 的动弦
的动弦![]() 过点
过点![]() ,过点
,过点![]() 且垂直于弦
且垂直于弦![]() 的直线交抛物线的准线于点
的直线交抛物线的准线于点![]() .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求![]() 的最小值.
的最小值.
【答案】(Ⅰ) ![]() (Ⅱ)2
(Ⅱ)2
【解析】
(Ⅰ)由椭圆求得右焦点,根据抛物线的焦点求出p的值,再写出抛物线C的标准方程;
(Ⅱ)①当动弦AB所在的直线斜率不存在时,求得![]() 2;②当动弦AB所在的直线斜率存在时,写出AB所在直线方程,与抛物线方程联立求出弦长|AB|;写出FM所在的直线方程,与抛物线方程联立求出弦长|MF|,再求
2;②当动弦AB所在的直线斜率存在时,写出AB所在直线方程,与抛物线方程联立求出弦长|AB|;写出FM所在的直线方程,与抛物线方程联立求出弦长|MF|,再求![]() 的最小值,从而得出结论.
的最小值,从而得出结论.
(Ⅰ)由椭圆方程得,椭圆的右焦点为![]()
∴抛物线的焦点为![]() ,∴
,∴![]() ,抛物线的标准方程为
,抛物线的标准方程为![]() .
.
(Ⅱ)①当动弦![]() 所在直线的斜率不存在时,易得:
所在直线的斜率不存在时,易得:
![]() ,
,![]() ,
,![]() .
.
②当动弦![]() 所在的直线斜率存在时,易知,
所在的直线斜率存在时,易知,![]() 的斜率不为0.
的斜率不为0.
设![]() 所在直线方程为
所在直线方程为![]() ,且
,且![]() ,
,![]() .
.
联立方程组:![]() ,得
,得![]() ;
;
![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]() 所在的直线方程为
所在的直线方程为![]() ,联立方程组:
,联立方程组: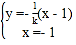 ,得点
,得点![]() ,
,
∴![]()
∴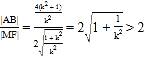 ,
,
综上所述:![]() 的最小值为2.
的最小值为2.

练习册系列答案
相关题目