题目内容
【题目】设
为正整数，记平面点集
.问：平面内最少要有多少条直线，它们的并集才能包含
，但不含点
?
【答案】至少需要
条直线.
【解析】
至少需要条直线.
容易发现，条直线满足要求.例如，直线
和
，易见，这条直线的并集包含
但不含原点.
另外的例子是直线集
.
下面证明：为最小可能数.
假设平面内
条直线的并集包含，但不包含原点，设其方程为
.
考虑多项式
.
则其阶为，且对任意
，有
，
.
记
，并记
为
被
除的余式.
由多项式以
为
个零点，知
对所有
均成立.
注意到，
.
故
，且显然有
.
将多项式表示成
的降幂形式
.
因为
，所以，
不为零多项式.
又当
时，
.
故有
个根.
于是，
，这表明，
不为零多项式.
又对于
，当时，均有
..
这表明，
至少有个根.
而
，则为零多项式.
故对于任意，
.
于是，
至少有个根.
而不为零多项式，因此，
.
于是，
.
进而，
.
综上，至少要条直线才能满足题设条件.
练习册系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费
和年销售量
（
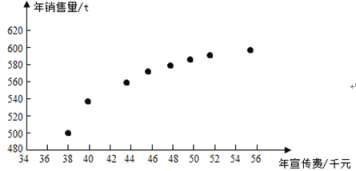
）数据作了初步处理，得到下面的散点图及一些统计量的值．
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中
，
（1）根据散点图判断，
与
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？给出判断即可，不必说明理由
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
（3）已知这种产品的年利润z与x、y的关系为
根据（2）的结果回答下列问题：
①年宣传费
时，年销售量及年利润的预报值是多少？
②年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据
，其回归线
的斜率和截距的最小二乘估计分别为：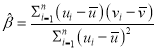
，
．
