题目内容
已知二面角α-l-β的大小为60°，直线m、n满足m⊥α，n⊥β，则异面直线m、n所成的角为 ．
考点：异面直线及其所成的角
专题：空间角
分析：由条件m⊥α，n⊥β可知m、n所成的夹角与二面角α-l-β所成的角相等或互补，而异面直线所成角的范围是0°＜θ≤90°，所以m、n所成的角为二面角α-l-β所成的角．
解答：
解：∵m⊥α，n⊥β，
∴m、n所成的夹角与二面角α-l-β所成的角相等或互补．
∵二面角α-l-β为60°，
∴异面直线m、n所成的角为60°．
故答案为60°，
∴m、n所成的夹角与二面角α-l-β所成的角相等或互补．
∵二面角α-l-β为60°，
∴异面直线m、n所成的角为60°．
故答案为60°，
点评：本题考查了异面直线所成角、二面角的平面角的作法和直线与平面垂直的判定与性质等知识点，属于中档题．运用垂面法作二面角的平面角，是解决本题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
定义[x]表示不超过x的最大整数，若f（x）=cos（x-[x]），则下列结论中：
①y=f（x）为偶函数；
②y=f（x）为周期函数，周期为2π；
③y=f（x）的最小值为cos1，无最大值；
④y=f（x）无最小值，最大值为1．
正确的命题的个数为（ ）
①y=f（x）为偶函数；
②y=f（x）为周期函数，周期为2π；
③y=f（x）的最小值为cos1，无最大值；
④y=f（x）无最小值，最大值为1．
正确的命题的个数为（ ）
| A、0个 | B、1个 | C、3个 | D、4个 |
设a，b，c为正数，a+b+9c2=1，则
+
+
c的最大值是（ ）
| a |
| b |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A（2，1），抛物线y2=4x的焦点是F，若抛物线上存在一点P，使得|PA|+|PF|最小，则P点的坐标为（ ）
| A、（2，1） | ||
| B、（1，1） | ||
C、(
| ||
D、(
|
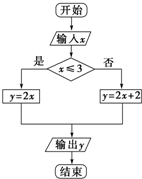根据如图的框图回答后面的问题．