题目内容
抛物线y2=4x上一点P到直线x=-1的距离与到点Q(2,2)的距离之差的最大值为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:当P,Q,F共线时,P到直线x=-1的距离与到点Q(2,2)的距离之差取最大值,由此能求出结果.
解答:
解: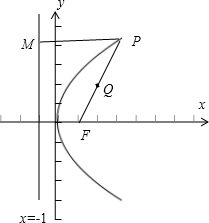 如图,由抛物线的定义知:
如图,由抛物线的定义知:
抛物线y2=4x上一点P到直线x=-1的距离|PM|=|PF|,
∴当P,Q,F共线时,
P到直线x=-1的距离与到点Q(2,2)的距离之差取最大值,
∵F(1,0),Q(2,2),
∴[|PM|-|PQ|]max
=[|PF|-|PQ|]max
=|QF|
=
=
,
故答案为:
.
 如图,由抛物线的定义知:
如图,由抛物线的定义知:抛物线y2=4x上一点P到直线x=-1的距离|PM|=|PF|,
∴当P,Q,F共线时,
P到直线x=-1的距离与到点Q(2,2)的距离之差取最大值,
∵F(1,0),Q(2,2),
∴[|PM|-|PQ|]max
=[|PF|-|PQ|]max
=|QF|
=
| (2-1)2+22 |
| 5 |
故答案为:
| 5 |
点评:本题考查两线段之差的最大值的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 15 |
| a |
| b |
| 11 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
已知-
<α<β<
,则
的范围是( )
| π |
| 2 |
| π |
| 2 |
| α-β |
| 2 |
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|