题目内容
18．在△ABC中，AB=3，AC=4，BC=5，AM⊥BC于M，点N是△ABC内部或边上一点，求$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值．分析 如图所示，直线BC方程为$\frac{x}{3}+\frac{y}{4}$=1，化为$y=-\frac{4}{3}x$+4，．直线AM的方程为：y=$\frac{3}{4}$x．联立解得M$（\frac{48}{25}，\frac{36}{25}）$．设N（x，y），则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y≤12}\end{array}\right.$．设$\overrightarrow{AM}$•$\overrightarrow{AN}$=$\frac{48}{25}x+\frac{36}{25}y$=t，
则y=$-\frac{4}{3}x$+$\frac{25t}{36}$，利用线性规划有关知识即可得出．
解答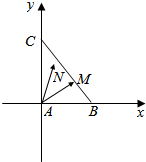 
解：如图所示，
直线BC方程为$\frac{x}{3}+\frac{y}{4}$=1，化为$y=-\frac{4}{3}x$+4，．
∴直线AM的方程为：y=$\frac{3}{4}$x．
联立$\left\{\begin{array}{l}{y=-\frac{4}{3}x+4}\\{y=\frac{3}{4}x}\end{array}\right.$，解得M$（\frac{48}{25}，\frac{36}{25}）$．
设N（x，y），则$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤4}\\{4x+3y≤12}\end{array}\right.$．
设$\overrightarrow{AM}$•$\overrightarrow{AN}$=$\frac{48}{25}x+\frac{36}{25}y$=t，
则y=$-\frac{4}{3}x$+$\frac{25t}{36}$，
∴当上述直线与BC重合时，y=$-\frac{4}{3}x$+$\frac{25t}{36}$在y轴上的截距$\frac{25t}{36}$取得最大值4，
∴t=$\frac{144}{25}$．
∴$\overrightarrow{AM}$•$\overrightarrow{AN}$的最大值为$\frac{144}{25}$．
点评 本题考查了向量的数量积运算性质、线性规划有关知识，考查了推理能力与计算能力，属于中档题．
| A． | （0，$\frac{1}{2}$] | B． | [$\frac{1}{2}，1$） | C． | [$\frac{1}{2}$，$\frac{3}{4}$] | D． | [$\frac{3}{4}$，1） |