题目内容
13.求函数y=sin($\frac{π}{6}$-x)的单调递减区间.分析 根据三角函数的单调性进行求解即可.
解答 解:y=sin($\frac{π}{6}$-x)=-sin(x-$\frac{π}{6}$),
要求函数y=sin($\frac{π}{6}$-x)的单调递减区间.
即求出y=sin(x-$\frac{π}{6}$)的单调递增区间,
由2kπ-$\frac{π}{2}$≤x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,
得2kπ-$\frac{π}{3}$≤x≤2kπ+$\frac{2π}{3}$,k∈Z,
即函数的单调递减区间为[2kπ-$\frac{π}{3}$,2kπ+$\frac{2π}{3}$],k∈Z.
点评 本题主要考查三角函数的单调区间的求解,根据正弦函数的单调性是解决本题的关键.

练习册系列答案
相关题目
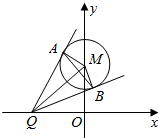 如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.
如图,已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别与圆M切于点AB.