题目内容
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为60°，且|$\overrightarrow{a}$|=1，|2$\overrightarrow{a}$+$\overrightarrow{b}$|=2$\sqrt{3}$，则|$\overrightarrow{b}$|=2．分析 由题意可得|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{4\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{4+4×1×|\overrightarrow{b}|×cos60°{+\overrightarrow{b}}^{2}}$=2$\sqrt{3}$，由此求得|$\overrightarrow{b}$|的值．
解答 解：向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为60°，且|$\overrightarrow{a}$|=1，
∵|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{（2\overrightarrow{a}+\overrightarrow{b}）}^{2}}$=$\sqrt{{4\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{4+4×1×|\overrightarrow{b}|×cos60°{+\overrightarrow{b}}^{2}}$=2$\sqrt{3}$，
求得|$\overrightarrow{b}$|=2，
故答案为：2．
点评 本题主要考查两个向量的数量积的定义的应用，求向量的模的方法，属于基础题．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
15．直线y=kx与双曲线4x2-y2=16不可能（ ）
| A． | 相交 | B． | 只有一个交点 | C． | 相离 | D． | 有两个公共点 |
13．某日用品按行业质量标准分成五个等级，等级系数依次为1，2，3，4，5．现从一批日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如表所示：
（1）求a，b，c的值；
（2）从等级为4的2件日用品和等级为5的3件日用品中任取两件（假定每件日用品被取出的可能性相同），写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率．
| 等级 | 频数 | 频率 |
| 1 | c | a |
| 2 | 4 | b |
| 3 | 9 | 0.45 |
| 4 | 2 | 0.1 |
| 5 | 3 | 0.15 |
| 合计 | 20 | 1.00 |
（2）从等级为4的2件日用品和等级为5的3件日用品中任取两件（假定每件日用品被取出的可能性相同），写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率．
20．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈R），则“$φ=\frac{π}{2}$”是“f（x）是偶函数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
10．设函数$f（x）=\left\{\begin{array}{l}（a-2）x，（x≤2）\\{2^x}-1，（x＞2）\end{array}\right.$是R上的单调递增函数，则实数a的取值范围为（ ）
| A． | （2，+∞） | B． | （-∞，$\frac{7}{2}$] | C． | （2，$\frac{7}{2}$） | D． | （2，$\frac{7}{2}]$ |
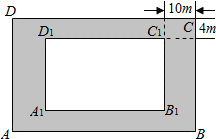如图，某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1和环公园人行道（阴影部分）组成，已知人行道的宽分别为4m和10m