题目内容
【题目】中山某学校的场室统一使用“欧普照明”的一种灯管，已知这种灯管使用寿命
（单位：月）服从正态分布
，且使用寿命不少于
个月的概率为
，使用寿命不少于
个月的概率为
.
（1）求这种灯管的平均使用寿命
；
（2）假设一间课室一次性换上
支这种新灯管，使用
个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.
【答案】：（1）18个月；（2）
（写成0.1808也可以）.
【解析】试题分析：（1）根据题意
,显然
，结合正态分布密度函数的对称性可知， 
，从而得出每支这种灯管的平均使用寿命；（2）先算出每支灯管使用
个月时已经损坏的概率，假设使用
个月时该功能室需要更换的灯管数量为
支，则
，独立重复使用概率公式概以及对事件的概率公式可得出至少两支灯管需要更换的概率.
试题解析：（1）∵
， 
， 
，∴
，
显然
由正态分布密度函数的对称性可知， 
，
即每支这种灯管的平均使用寿命是
个月；
（2）每支灯管使用
个月时已经损坏的概率为
，
假设使用
个月时该室需更换的灯管数量为
支，则
故至少两支灯管需要更换的概率
（写成0.1808也可以）.
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
为参数），在以原点为极点， 
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．
（1）求曲线
的普通方程和直线
的倾斜角；
（2）设点
，直线
和曲线
交于
两点，求
的值．
【题目】韩国民意调查机构“盖洛普韩国”2016年11月公布的民调结果显示，受“闺蜜门”时间影响，韩国总统朴槿惠的民意支持率持续下跌，在所调查的1000个对象中，年龄在[20，30）的群体有200人，支持率为0%，年龄在[30，40）和[40，50）的群体中，支持率均为3%；年龄在[50，60）和[60，70）的群体中，支持率分别为6%和13%，若在调查的对象中，除[20，30）的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为100的等差数列．
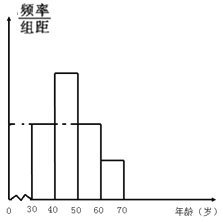
(1)依频率分布直方图求出图中各年龄层的人数
（2）请依上述支持率完成下表：
年龄分布 是否支持 | [30，40）和[40，50） | [50，60）和[60，70） | 合计 |
支持 | |||
不支持 | |||
合计 |
根据表中的数据，能否在犯错误的概率不超过0.001的前提下认为年龄与支持率有关？
附表：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
，其中
参考数据：125×33=15×275，125×97=25×485）
