题目内容
14.已知圆O的半径为r,A为平面上一点,|OA|=a,a≠r,P是圆上任意一点,线段AP的垂直平分线与直线OP相交于点Q,以OA的中点为原点,OA所在直线为x轴建立平面直角坐标系,若Q点轨迹的离心率为$\sqrt{5}$,则( )| A. | a=$\sqrt{5}$r | B. | a=2r | C. | a=$\sqrt{3}$r | D. | a=$\sqrt{2}$r |
分析 根据双曲线的定义,可知点Q的轨迹是:以O,A为焦点,OP为实轴长的双曲线,求出离心率,即可得出结论.
解答 解:由题意,A为⊙O外一定点,P为⊙O上一动点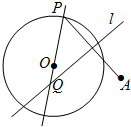
∵线段AP的垂直平分线交直线OP于点Q,
∴QA=QP,∴QA-Q0=QP-QO=OP=r,
即动点Q到两定点O、A的距离差为定值,
根据双曲线的定义,可知点Q的轨迹是:以O,A为焦点,OP为实轴长的双曲线
∴$\frac{a}{r}$=$\sqrt{5}$,
∴a=$\sqrt{5}$r,
故选:A.
点评 结合双曲线的定义及圆与直线的相关性质,推导新的结论,熟练掌握双曲线的定义及圆与直线的性质是解决问题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.设m、n是两条不同的直线,α、β是两个不同的平面,下列四个命题正确的是( )
| A. | 若m、n?α,m∥β,n∥β,则α∥β | B. | 若m?α,α∥β,则m∥β | ||
| C. | 若m⊥α,α⊥β,n∥β,则m⊥n | D. | 若α⊥γ,β⊥γ,则α⊥β |
6.设集合M={x|y=ln(1-x)},集合N={y|y=x2},则M∩N等于( )
| A. | [0,1) | B. | [0,1] | C. | (一∞,1) | D. | (一∞,1] |
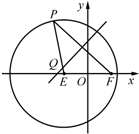 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.