题目内容
12.已知圆C过点O(0,0),A(-1,-7)和B(8,-4)(Ⅰ)求圆C的方程;
(Ⅱ)求与AB垂直且被圆C截得弦长等于|AB|的直线l的方程.
分析 (Ⅰ)设出圆的标准方程,代入三个点的坐标,求得D,E,F则圆的方程可得.
(Ⅱ)设出直线l的方程,利用点到直线的距离求得m,则可求得直线的方程.
解答 解:(Ⅰ)设圆C的方程为x2+y2+Dx+Ey+F=0.
因为O,A,B三点都在圆C上,所以它们的坐标都是圆C方程的解,
故$\left\{\begin{array}{l}F=0\\ 50-D-7E+F=0,80+8D-4E+F=0\end{array}$解此方程组,得D=-6,E=8,F=0.
故所求圆C的方程为x2+y2-6x+8y=0.
(Ⅱ)直线AB的方程为x-3y-20=0,故设直线l的方程为3x+y+m=0.
由题意,圆心C(3,-4)到直线AB与直线l的距离相等,
故有$\frac{|3-3×(-4)-20|}{\sqrt{12+(-3)2}}$=$\frac{|3×3+(-4)+m|}{\sqrt{32+12}}$,
解得m=0或m=-10.
所以直线l的方程为3x+y=0或3x+y-10=0.
点评 本题主要考查了直线与圆的问题的综合运用.考查了学生分析问题和基本的运算能力.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
14.已知圆O的半径为r,A为平面上一点,|OA|=a,a≠r,P是圆上任意一点,线段AP的垂直平分线与直线OP相交于点Q,以OA的中点为原点,OA所在直线为x轴建立平面直角坐标系,若Q点轨迹的离心率为$\sqrt{5}$,则( )
| A. | a=$\sqrt{5}$r | B. | a=2r | C. | a=$\sqrt{3}$r | D. | a=$\sqrt{2}$r |
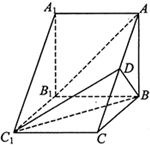 在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.
在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.