题目内容
4.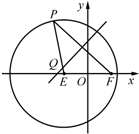 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.(1)求动点Q的轨迹Γ的方程;
(2)设直线l与(1)中轨迹Г相交于A,B两点,直线OA,l,OB的斜率分别为k1,k,k2(其中k>0),若恰好成等比数列,求△OAB的面积S的最大值.
分析 (Ⅰ)由题意易得|QE|+|QF|=4,由椭圆的定义可得;
(Ⅱ)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2).与椭圆方程联立可得(1+4k2)x2+8kmx+4m2-4=0,由韦达定理和等比数列可解得k=$\frac{1}{2}$,可得面积S=$\sqrt{2-{m}^{2}}$|m|=$\sqrt{(2-{m}^{2}){m}^{2}}$,由基本不等式可得最值.
解答 解:(Ⅰ)连接QF,由垂直平分线的性质可得|QP|=|QF|,
则|QE|+|QF|=|QE|+|QP|=|EP|=4,
∴动点Q的轨迹Γ是以E,F为焦点,长轴长为4的椭圆.
可知a=2,c=$\sqrt{3}$,故b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
∴点Q的轨迹Γ的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)设直线l的方程为y=kx+m,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y并整理可得(1+4k2)x2+8kmx+4m2-4=0,
∴△=16(1+4k2-m2)>0,x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4({m}^{2}-1)}{1+4{k}^{2}}$,
∵k1,k,k2构成等比数列,
∴k2=k1k2=$\frac{(k{x}_{1}+m)(k{x}_{2}+m)}{{x}_{1}{x}_{2}}$,化简变形可得km(x1+x2)+m2=0,
∴-km$\frac{8km}{1+4{k}^{2}}$+m2=0,解得k2=$\frac{1}{4}$.∵k>0,∴k=$\frac{1}{2}$.
此时△=16(2-m2)>0,解得-$\sqrt{2}$<m<$\sqrt{2}$.
又由A、O、B三点不共线得m≠0,∴-$\sqrt{2}$<m<$\sqrt{2}$且m≠0,
∴S=$\frac{1}{2}$|AB|d=$\frac{1}{2}$$\sqrt{1+{k}^{2}}$|x1-x2|•$\frac{|m|}{\sqrt{1+{k}^{2}}}$
=$\frac{1}{2}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$|m|=$\sqrt{2-{m}^{2}}$|m|
=$\sqrt{(2-{m}^{2}){m}^{2}}$≤$\frac{2-{m}^{2}+{m}^{2}}{2}$=1
当且仅当2-m2=m2即m=±1时取等号,
∴△OAB的面积S的最大值为1
点评 本题考查直线与圆锥曲线的综合应用,设计轨迹方程的求解和圆锥曲线的最值,属难题.

| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
| A. | $\frac{3π}{4}$ | B. | π | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
| A. | 4320 | B. | -4320 | C. | 20 | D. | -20 |
| A. | a=$\sqrt{5}$r | B. | a=2r | C. | a=$\sqrt{3}$r | D. | a=$\sqrt{2}$r |
 教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.
教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.