题目内容
【题目】判断下列两圆的位置关系.
(1)C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0;___________
(2)C1:x2+y2-2y=0,C2:x2+y2-2![]() x-6=0;___________
x-6=0;___________
(3)C1:x2+y2-4x-6y+9=0,C2:x2+y2+12x+6y-19=0;___________
(4)C1:x2+y2+2x-2y-2=0,C2:x2+y2-4x-6y-3=0.___________
(5)x2+y2=9和x2+y2-8x+6y+9=0 ________________
(6)圆C1:x2+y2-2x-6y-6=0与圆C2:x2+y2-4x+2y+4=0______
(7)圆x2+y2+6x-7=0和圆x2+y2+6y-27=0 ____________
【答案】相交内切外切相交相交相交相交
【解析】
将两圆方程化为标准方程,再根据圆心之间距离与两半径和与差的关系确定两圆位置关系.
(1)![]()
![]() ,因此两圆相交;
,因此两圆相交;
(2)![]()
![]() ,因此两圆内切;
,因此两圆内切;
(3)![]()
![]() ,因此两圆外切;
,因此两圆外切;
(4)![]()
![]() ,因此两圆相交;
,因此两圆相交;
(5)![]()
![]() ,因此两圆相交;
,因此两圆相交;
(6)![]()
![]() ,因此两圆相交;
,因此两圆相交;
(7)![]()
![]() ,因此两圆相交;
,因此两圆相交;

【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
【题目】A、B、C三个班共有100名学生,为调查他们的体育锻炼情况,通过分层抽样获得了部分学生一周的锻炼时间,数据如下表(单位:小时);
A班 | 6 6.5 7 7.5 8 |
B班 | 6 7 8 9 10 11 12 |
C班 | 3 4.5 6 7.5 9 10.5 12 13.5 |
(1)试估计C班的学生人数;
(2)从A班和C班抽出的学生中,各随机选取一人,A班选出的人记为甲,C班选出的人记为乙,假设所有学生的锻炼时间相对独立,求该周甲的锻炼时间比乙的锻炼时间长的概率;
(3)再从A、B、C三个班中各随机抽取一名学生,他们该周的锻炼时间分别是7,9,8.25(单位:小时),这3个新数据与表格中的数据构成的新样本的平均数记 ![]() ,表格中数据的平均数记为
,表格中数据的平均数记为 ![]() ,试判断
,试判断 ![]() 和
和 ![]() 的大小,(结论不要求证明)
的大小,(结论不要求证明)
【题目】某车间为了规定工时定额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间![]() 与零件个数
与零件个数![]() 之间有较好的相关关系.
之间有较好的相关关系.
(1)求加工时间与零件个数的线性回归方程![]() .
.
(2)试预报加工10个零件需要的时间.
附录:参考公式: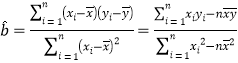 ,
,![]() .
.
