题目内容
7.已知整数x,y满足不等式组$\left\{\begin{array}{l}{x+2y+2≤0}\\{2x-y+1≥0}\end{array}\right.$,设z=2x-3y,则( )| A. | z有最大值1,无最小值 | B. | z有最大值2,无最小值 | ||
| C. | z有最小值1,无最大值 | D. | z有最小值2,无最大值 |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答 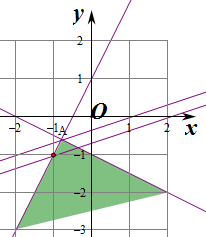 解:由z=x-3y得y=$\frac{2}{3}$x-$\frac{z}{3}$,
解:由z=x-3y得y=$\frac{2}{3}$x-$\frac{z}{3}$,
作出不等式组对应的平面区域如图(阴影部分):
平移直线y=$\frac{2}{3}$x-$\frac{z}{3}$,
由图象可知当直线y=$\frac{2}{3}$x-$\frac{z}{3}$经过点A时,直线y=$\frac{2}{3}$x-$\frac{z}{3}$的截距最大,
此时z最小,
由 $\left\{\begin{array}{l}{x+2y+2=0}\\{2x-y+1=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{x=-\frac{4}{5}}\\{y=-\frac{3}{5}}\end{array}\right.$,即A(-$\frac{4}{5}$,-$\frac{3}{5}$)
∵x是整数,∴A点坐标不满足条件,
则当x=-1时,y=-1,此时代入目标函数z=2x-3y,
得z=-2×1-3×(-1)=3-2=1.
∴目标函数z=2x-3y的最小值是1.
故选:C.
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
17.为了得到函数$y=sin(x-\frac{π}{3})(x∈R)$的图象,只需把函数y=sinx的图象上所有的点( )
| A. | 向右平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
15.某海滨浴场的海浪高度y (米)是时间t(0≤t≤24)(小时)的函数,记作y=f(t),表是某天各时的浪高数据:
(1)选用一个函数来近似描述这个海滨浴场的海浪高度y (米)与t时间(小时)的函数关系;
(2)依据规定,当海浪高度不少于1米时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的上午8时至晚上20时之间,有多少时间可供冲浪爱好者进行冲浪?
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(2)依据规定,当海浪高度不少于1米时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的上午8时至晚上20时之间,有多少时间可供冲浪爱好者进行冲浪?
2.已知数列{an}中,a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{\sqrt{3}{a}_{n}+1}$(n∈N*),则a1+a2+…+a2015=( )
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 1008$\sqrt{3}$ |
19.计算$\frac{5}{i-2}$(i为虚数单位)的值是( )
| A. | i+2 | B. | i-2 | C. | -2-i | D. | 2-i |
16.下表是关于出生男婴与女婴调查的列联表:
那么A=47,B=82.
| 晚上 | 白天 | 总计 | |
| 男婴 | 45 | A | 92 |
| 女婴 | 53 | 35 | 88 |
| 总计 | 98 | B | 180 |