题目内容
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)令![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅲ)若![]() ,正实数
,正实数![]() ,
, ![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)0;(2)详见解析;(3)证明详见解析.
【解析】试题分析:(1)由导数几何意义得切线斜率![]() ,所以先求导数得
,所以先求导数得![]() ,即
,即![]() ,又
,又![]() ,再根据点斜式得切线方程
,再根据点斜式得切线方程![]() (2)先求导数
(2)先求导数![]() ,再分类讨论导函数在定义区间上符号变化规律,确定极值取法:当
,再分类讨论导函数在定义区间上符号变化规律,确定极值取法:当![]() 时,
时, ![]() ,函数
,函数![]() 无极值点.当
无极值点.当![]() 时,一个零点
时,一个零点![]() ,导函数在其左右符号变化,先增后减,所以
,导函数在其左右符号变化,先增后减,所以![]() 有极大值,无极小值
有极大值,无极小值
(3)先化简![]() 为
为![]() ,转化为关于
,转化为关于![]() 函数关系式:
函数关系式: ![]() ,研究函数
,研究函数![]() ,其中
,其中![]() ,得
,得![]() ,因此
,因此![]() ,解不等式得
,解不等式得![]()
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ,所以切点为
,所以切点为![]() ,
,
又![]() ,则切线斜率
,则切线斜率![]() ,
,
故切线方程为![]() ,即
,即![]() ................3分
................3分
(2)![]() ,
,
则![]() ,......................4分
,......................4分
当![]() 时,∵
时,∵![]() ,∴
,∴![]() .
.
∴![]() 在
在![]() 上是递增函数,函数
上是递增函数,函数![]() 无极值点..................5分
无极值点..................5分
当![]() 时,
时, 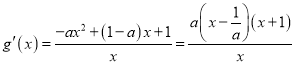 ,令
,令![]() 得
得![]() ,
,
∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
因此![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,............................7分
上是减函数,............................7分
∴![]() 时,
时, ![]() 有极大值
有极大值![]() ,
,
综上,当![]() 时,函数
时,函数![]() 无极值;
无极值;
当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,无极小值............................... 8分
,无极小值............................... 8分
(3)证明:当![]() 时,
时, ![]() ,
,
由![]() ,即
,即![]() ,
,
从而![]() ,
,
令![]() ,则由
,则由![]() 得:
得: ![]() ,
,
可知, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .....................12分
.....................12分

【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
【题目】某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另外15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另外30人比较粗心.
(1)试根据上述数据完成![]() 列联表;
列联表;
数学成绩及格 | 数学成绩不及格 | 合计 | |
比较细心 | 45 | ||
比较粗心 | |||
合计 | 60 | 100 |
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系?
参考数据:独立检验随机变量![]() 的临界值参考表:
的临界值参考表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]()
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见下图)
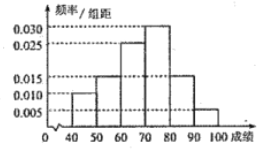
(Ⅰ)求所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
列联表,能否有超过95%的把握认为“获奖与学生的文理科有关”?
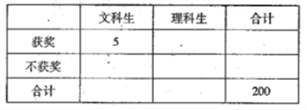
附表及公式:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |