题目内容
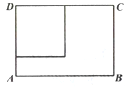
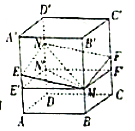
【题目】如图所示, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() 平面
平面![]() ,且
,且![]() 在平面
在平面![]() 的同侧,它们在
的同侧,它们在![]() 内的正射影分别是
内的正射影分别是![]() ,且
,且![]() 是
是![]() ,
, ![]() 到
到![]() 的距离为
的距离为![]() .
.
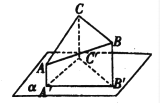
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() ,推导出
,推导出![]() ,由此能求出
,由此能求出![]() 到平面
到平面![]() 的距离.
的距离.
(2)以![]() 为原点,射线
为原点,射线![]() 分别为
分别为![]() 轴正方向建立空间直角坐标系,利用向量法能求出平面
轴正方向建立空间直角坐标系,利用向量法能求出平面![]() 与平面
与平面![]() 所成较小二面角的余弦值.
所成较小二面角的余弦值.
试题解析:
(1)如图,过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() .由题意知
.由题意知![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() 或
或![]() (舍),∴点
(舍),∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(2)以![]() 为原点,射线
为原点,射线![]() 分别为
分别为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
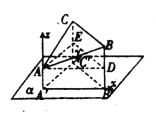
由(1)可知![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则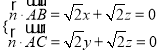 取
取![]() ,得
,得![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则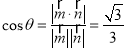 ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

【题目】空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2017年1月某日某省x个监测点数据统计如下:
空气污染指数 (单位:μg/m3) |
|
|
|
|
监测点个数 | 15 | 40 | y | 10 |
(1)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
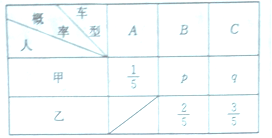
(2)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?