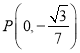题目内容
【题目】某商场销售一种水果的经验表明，该水果每日的销售量
（单位：千克）与销售价格
（单位：元/千克）满足关系式
，其中
，
为常数.已知销售价格为6元/千克时，每日可售出该水果52千克.
（1）求的值；
（2）若该水果的成本为5元/千克，试确定销售价格的值，使商场每日销售该水果所获得的利润最大，并求出最大利润.
【答案】（1）
；（2）
，66元.
【解析】
（1）由销售价格为6元/千克时，每日可售出该水果52千克；建立方程，即可求出
的值；
（2）商场每日销售该水果所获得的利润
每日的销售量
销售该水果的单利润，可得日销售量的利润函数为关于
的三次多项式函数，再用求导数的方法讨论函数的单调性，得出函数的极大值点，从而得出最大值对应的值.
（1）因为
时，
，所以
，.
（2）由（1）可知，该水果每日的销售量为
，
所以商场每日销售该水果所获得的利润为
，
，
从而
，
于是，当变化时，
，
的变化情况如下表：
|
| 7 |
|
| + | 0 | - |
| 单调递增 | 极大值66 | 单调递减 |
由上表可得，时，函数取得极大值，也是最大值.
所以，当销售价格为7元/千克时，商场每日销售该水果所获得的利润最大，为66元.
练习册系列答案
相关题目
