题目内容
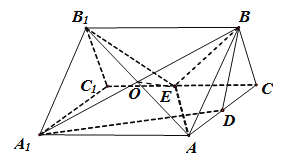
【题目】如图,三棱柱![]() 的所有棱长都是2,
的所有棱长都是2,![]() 面
面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
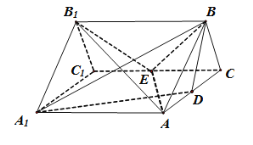
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出![]() ,从而平面
,从而平面![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() ,
,![]() ,再求出
,再求出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)本问方法较多,可用割补法,转换顶点法,构造法等,其中割补法较为方便,将![]() 转化为
转化为![]() ,即可求解.
,即可求解.
解:(1)∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵三棱柱![]() 中
中![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵在正方形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
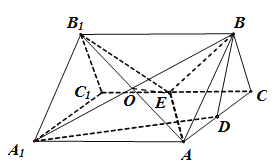
(2)解法一(割补法):
![]()
![]()
![]() .
.
解法二(利用平行顶点轮换):
∵![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
解法三(利用对称顶点轮换):
连结![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
∴![]()
![]() .
.
解法四(构造法):
连结![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,再连结
的中点,再连结![]() .
.
由题意知在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,
,
∴![]() 面
面![]() ,
,
∴![]()
![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目