题目内容
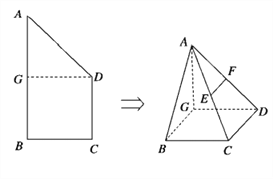
【题目】如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.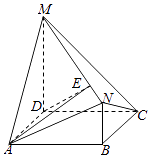
(1)过B作平面BFG∥平面MNC,平面BFG与CD、DM分别交于F、G,求AF与平面MNC所成角的正弦值;
(2)E为直线MN上一点,且平面ADE⊥平面MNC,求 ![]() 的值.
的值.
【答案】
(1)解:当CF=MG=1时,平面BFG∥平面MNC.
证明:连接BF,FG,GB,∵BN=GM=1,BN∥GM,∴四边形BNMG是平行四边形,∴BG∥NM,∵CD=MD,CF=MG,∴FG∥CM,∵BG∩FG=G,∴平面BFG∥平面MNC,
以D为原点,DA,DC,DM所在直线分别为x,y,z轴,建立空间直角坐标系(如图),则A(2,0,0),C(0,3,0),F(0,2,0),M(0,0,3),N(2,3,1),∴ ![]() =(﹣2,2,0),
=(﹣2,2,0), ![]() =(2,3,﹣2),
=(2,3,﹣2), ![]() =(0,3,﹣3),
=(0,3,﹣3),
设平面MNC的一个法向量 ![]() =(x,y,z),
=(x,y,z),
则 ![]() 令y=2,则z=2,x=﹣1,∴
令y=2,则z=2,x=﹣1,∴ ![]() =(﹣1,2,2),
=(﹣1,2,2),
设AF与平面MNC所成角为θ,则 ![]()
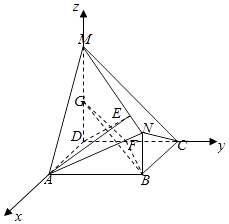
(2)解:设E(a,b,c), ![]() ,则
,则 ![]() =λ
=λ ![]() ,
,
∵ ![]() =(a,b,c﹣3),
=(a,b,c﹣3), ![]() =(2,3,﹣2),∴点E的坐标为(2λ,3λ,3﹣2λ),
=(2,3,﹣2),∴点E的坐标为(2λ,3λ,3﹣2λ),
∵AD⊥平面MDC,∴AD⊥MC,
欲使平面ADE⊥平面MNC,只要AE⊥MC,
∵ ![]() =(2λ﹣2,3λ,3﹣2λ),
=(2λ﹣2,3λ,3﹣2λ), ![]() =(0,3,﹣3),∴9λ﹣3(3﹣2λ)=0,得
=(0,3,﹣3),∴9λ﹣3(3﹣2λ)=0,得 ![]() ,∴
,∴ ![]() .
.
【解析】(1)先分析所给的条件,进而建立合适的空间直角坐标系,再利用向量法求AF与平面MNC所成角的正弦值;(2)根据“欲使平面ADE⊥平面MNC,只要AE⊥MC”的依据是:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
【考点精析】利用平面与平面平行的判定和平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
(Ⅰ)根据题目条件完成下面2×2列联表,并据此判断是否有99%的把握认为环保知识成绩优秀与学生的文理分类有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅱ)现已知A,B,C三人获得优秀的概率分别为 ![]() ,设随机变量X表示A,B,C三人中获得优秀的人数,求X的分布列及期望E(X).
,设随机变量X表示A,B,C三人中获得优秀的人数,求X的分布列及期望E(X).
附: ![]() ,n=a+b+c+d
,n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |