Question

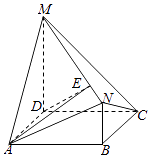
【题目】在正方体ABCD﹣A1B1C1D1中，E是A1B1上一点，若平面EBD与平面ABCD所成锐二面角的正切值为 ，设三棱锥A﹣A1D1E外接球的直径为a，则 = ．

Answer 1

【答案】
【解析】解：过E作EF∥AA1交AB于F，过F作FG⊥BD于G，连接EG，则∠EGF为平面EBD与平面AB﹣CD所成锐二面角的平面角，∵ ，∴ ，

设AB=3，则EF=3，∴ ，则BF=2=B1E，

∴A1E=1，则三棱锥A﹣A1D1E外接球的直径 ，

∴ ．

所以答案是 ．

【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)，还要掌握球内接多面体(球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长)的相关知识才是答题的关键．