题目内容
15.求函数f(x)=4x-2x+1,x∈[-3,2]的值域.分析 通过换元转化为求二次函数的值域问题,先求出函数的对称轴,得到函数的单调区间,求出函数的最大值和最小值即可求出值域.
解答 解:由于函数f(x)=4x-2x+1=(2x)2-2x+1
令t=2x,由于x∈[-3,2],则t∈[$\frac{1}{8}$,4],
由f(t)=t2-t+1=(t-$\frac{1}{2}$)2+$\frac{3}{4}$
得:f(t)的对称轴是t=$\frac{1}{2}$,
∴函数在[$\frac{1}{8}$,$\frac{1}{2}$]递减,在[$\frac{1}{2}$,4]递增,
∴f(t)最小值=f($\frac{1}{2}$)=$\frac{3}{4}$,f(t)最大值=f(4)=13,
∴函数的值域是[$\frac{3}{4}$,13].
点评 本题考查了求函数的值域问题,考查二次函数的性质,是一道基础题.

练习册系列答案
相关题目
6.长为2的线段AB的两个端点分别在x轴和y轴上滑动,那么线段AB中点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
3.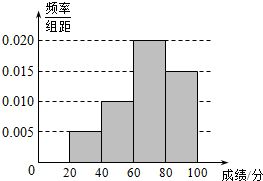 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
10.下列函数是偶函数,且在[0,1]上单调递增的是( )
| A. | y=cos(x+$\frac{π}{2}$) | B. | y=1-2cos22x | C. | y=-x2 | D. | y=|sin(π-x)| |
20.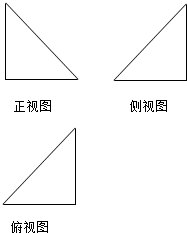 己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )
己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )
 己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )
己知几何体的三视图如图所示,它们都是直角边长等于1的等腰直角三角形,则这个几何体的表面积等于( )| A. | 2 | B. | $\frac{{3+\sqrt{2}}}{2}$ | C. | 4 | D. | $\sqrt{2}+1$ |
4.抛物线y=2x2的焦点坐标是( )
| A. | ($\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0) | C. | (0,$\frac{1}{8}$) | D. | (0,-$\frac{1}{8}$) |
5.已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A. | $\frac{3}{4}$πR2 | B. | $\frac{9}{2}$πR2 | C. | $\frac{9}{4}$πR2 | D. | $\frac{9}{8}$πR2 |