Question

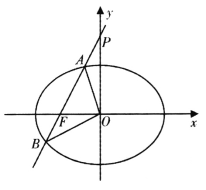
【题目】如图，为方便金湖县人民游览三河风景区附近的“网红桥”，现准备在河岸一侧建造一个观景台A，已知射线PM， PN为两边夹角为120°的公路(长度均超过5千米)，在两条公路PM，PN上分别设立游客上下点B、C，在观景台A和游客上下点B、C之间和游客上下点B、C之间分别建造三条观光线路AB，AC，BC，测得PB=3干米，PC=5千米.

（1）求线段BC的长度；

（2）若∠BAC= 60°，因政府要计算修建三条观光线路所需费用，所以要计算AB，AC，BC三条线路的总长度的取值范围，请你建立合适的数学模型，帮助政府解决这个问题.

Answer 1

【答案】（1）线段BC的长度为7千米；（2）

【解析】

（1）在△PBC中，利用余弦定理得到BC；
（2）设∠ABC＝，得到∠ACB＝120°，利用正弦定理将AC＋AB用表示，结合三角函数的有界性求范围.

解：（1）在△PBC中，

由余弦定理得，

，
所以线段BC的长度为7千米；
（2）设∠ABC＝，因为∠BAC= 60°，所以∠ACB＝120°，
在△ABC中，由正弦定理得，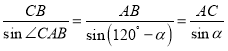
，
因为，
所以，

因此

，
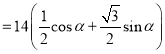
因为，所以 .

，则，

即，

，
所以AB，AC，BC三条线路的总长度的取值范围.