题目内容
2.P为椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1上一点,F1、F2分别为左、右焦点,若|PF1|,|F1F2|,|PF2|成等比数列,则△PF1F2的面积为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 4 | D. | 8 |
分析 通过设|PF1|=t,由椭圆定义可知|PF2|=8-t、|F1F2|=2c=4,利用|PF1|、|F1F2|、|PF2|成等比数列计算可知△PF1F2为等边三角形,进而计算可得结论.
解答 解:由椭圆定义可知|PF1|+|PF2|=2a=8,|F1F2|=2c=4,
设|PF1|=t,则|PF2|=8-t,
∵|PF1|、|F1F2|、|PF2|成等比数列,
∴$|{F}_{1}{F}_{2}{|}^{2}$=|PF1|•|PF2|,
∴16=t(8-t),
解得:t=4,
∴|PF1|=|PF2|=4,
∴△PF1F2为等边三角形,
∴${S}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}•4•4•\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
故选:B.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
10.已知a为如图所示的算法框图中输出的结果,则a的值为( )
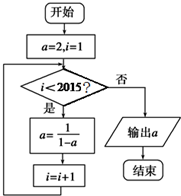

| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | -2 |
17.执行如图所示的程序框图,则输出的T值为( )
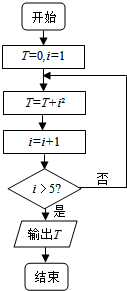

| A. | 30 | B. | 54 | C. | 55 | D. | 91 |