题目内容
【题目】已知椭圆![]() 的右焦点
的右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 分别是线段
分别是线段![]() 的中点试,判断直线
的中点试,判断直线![]() 是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 过定点
过定点![]()
【解析】
(1)由题意得 ,求出
,求出![]() ,即可求出椭圆方程;
,即可求出椭圆方程;
(2)设直线![]() 的方程为
的方程为![]() ,①当
,①当![]() 时,联立方程组
时,联立方程组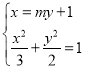 ,化简可得
,化简可得
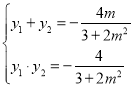 ,进而求出
,进而求出![]() ,同理可得
,同理可得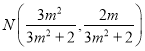 ,进而求出
,进而求出![]() ,求出直线
,求出直线![]() 的方程,求出必过的定点
的方程,求出必过的定点![]() ;②当
;②当![]() 时,易知直线
时,易知直线![]() 过定点
过定点![]() ;综上即可求出结果.
;综上即可求出结果.
解:(1)由题意得 ,∴
,∴ ,
,
∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)得![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,
①当![]() 时,由
时,由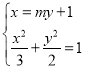 ,得
,得![]() ,
,
∴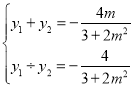 ,∴
,∴![]()
同理,由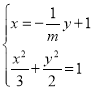 ,可得
,可得![]()
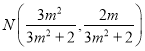
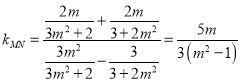
∴直线![]() 的方程为
的方程为 ,过定点
,过定点![]() ;
;
②当![]() 时,则直线
时,则直线![]() 的方程为
的方程为![]() ,
,
∴直线![]() 过定点
过定点![]()
综上,直线![]() 过定点
过定点![]()

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】“读书可以让人保持思想活跃,让人得到智慧启发,让人滋养浩然之气”,2018年第一期中国青年阅读指数数据显示,从供给的角度,文学阅读域是最多的,远远超过了其他阅读域的供给量.某校采用分层抽样的方法从1000名文科生和2000名理科生中抽取300名学生进行了在暑假阅读内容和阅读时间方面的调查,得到数据如表:
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 130 | ||
文科生 | 45 | ||
合计 |
(1)先完成上面的表格,并判断能否有90%的把握认为学生所学文理与阅读内容有关?
(2从300名被调查的学生中,随机进取30名学生,整理其日平均阅读时间(单位:分钟)如表:
阅读时间 |
|
|
|
|
|
男生人数 | 2 | 4 | 3 | 5 | 2 |
女生人数 | 1 | 3 | 4 | 3 | 3 |
试估计这30名学生日阅读时间的平均值(同一组中的数据以这组数据所在区间中点的值作代表)
(3)从(2)中日均阅读时间不低于120分钟的学生中随机选取2人介绍阅读心得,求这两人都是女生的概率.
参考公式: 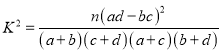 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务与责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准.为此,对全市家庭日常用水量的情况进行抽样抽查,获得了![]() 个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
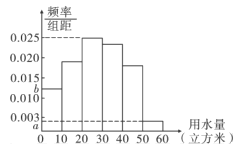
分组 | 频数 | 频率 |
| 25 | |
| 0.19 | |
| 50 | |
| 0.23 | |
| 0.18 | |
| 5 |
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)若以各组区间中点值代表该组的取值,试估计全市家庭年均用水量;
(3)从样本中年用水量在![]() (单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
(单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).