题目内容
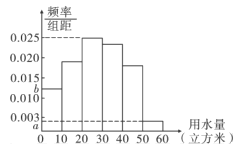
【题目】我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务与责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准.为此,对全市家庭日常用水量的情况进行抽样抽查,获得了![]() 个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
分组 | 频数 | 频率 |
| 25 | |
| 0.19 | |
| 50 | |
| 0.23 | |
| 0.18 | |
| 5 |
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)若以各组区间中点值代表该组的取值,试估计全市家庭年均用水量;
(3)从样本中年用水量在![]() (单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
(单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
【答案】(1)![]() ,
,![]() ,
,![]() (2)
(2)![]() (立方米)(3)
(立方米)(3)![]()
【解析】
(1)观察图和表,用水量在![]() 内的频数是50,频率是
内的频数是50,频率是![]() ,由此可求得样本容量
,由此可求得样本容量![]() ,再由相应的频率求出
,再由相应的频率求出![]() ;
;
(2)用每组中点值代表这组的估计值计算均值.
(3)可把五个家庭编号用列举法写出任取3个各种情况,同时得用水量最多的家庭被选中的情况,计数后可得概率.
解:(1)用水量在![]() 内的频数是50,频率是
内的频数是50,频率是![]() ,
,
则![]() ,
,
用水量在![]() 内的频率是
内的频率是![]() ,则
,则![]() ,
,
用水量在![]() 内的频率是
内的频率是![]() ,则
,则![]() ;
;
(2)估计全市家庭年均用水量为
![]() ;
;
(3)设![]() 代表年用水量从多到少的5个家庭,
代表年用水量从多到少的5个家庭,
从中任选3个,总的基本事件为![]() ,共10个,
,共10个,
其中包含![]() 的有
的有![]() ,共6个,
,共6个,
所以![]() ,即年用水量最多的家庭被选中的概率是
,即年用水量最多的家庭被选中的概率是![]() .
.

练习册系列答案
相关题目